经典的带环链表问题(链表补充)
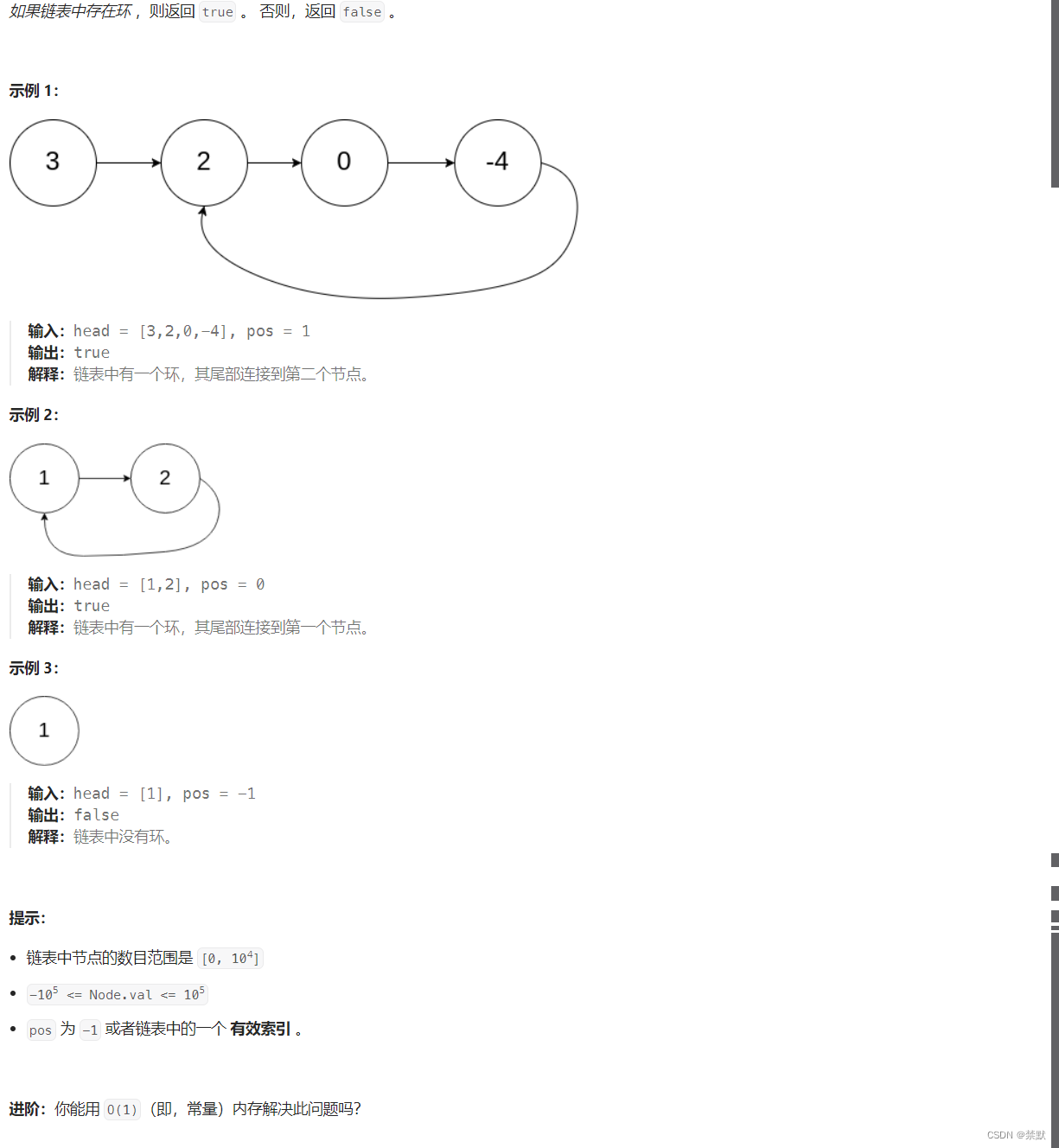
环形链表1
运用快慢指针的方法,fast ,slow从头节点出发,快指针走两步,慢指针走一步,若有环,快指针先进环,后续如果慢指针和快指针相遇,则链表带环。转换成了追击问题。
struct ListNode {
int val;
struct ListNode *next;
};
typedef struct ListNode LN;
bool hasCycle(struct ListNode *head) {
LN*slow,*fast;
slow=fast=head;
while(fast && fast->next){
slow=slow->next;
fast=fast->next->next;
if(slow==fast)
return true;
}
return false;
}
思考:为什么一定会相遇,会不会错过,永远追不上?若快指针走三步,四步呢?
证明:假设链表就是有环,slow(1步)进环时,fast(两步)与slow的距离为N,追击过程中,每走一次,N都会-1,最后到0。本题的思想证明,距离为0就是追上了。
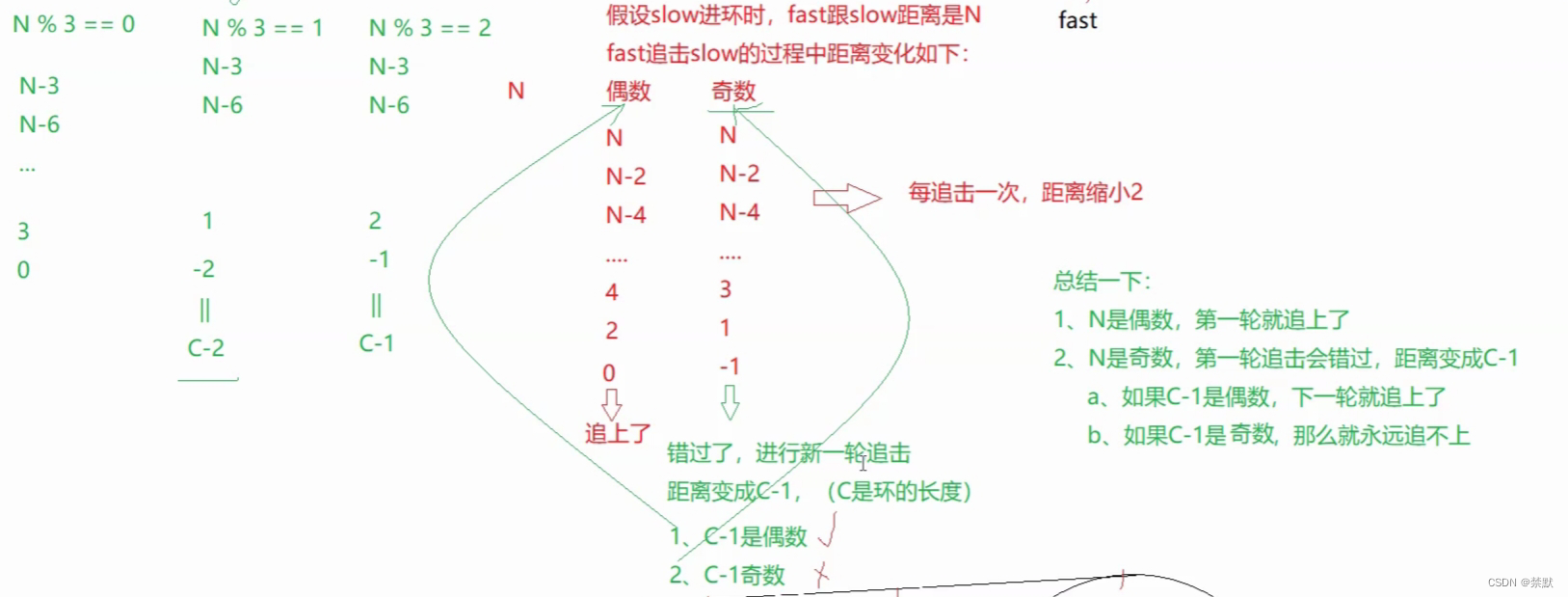
若fast走三步,同样假设slow进环时,fast与slow相差N,
fast追击slow过程中,距离变化一直-2,但是最后结果要注意,N为偶数时,最后变为0,N为奇数时,最后为-1.而当距离为-1时,两指针会错过,进行新一轮追击。这时假设环的长度为C。新的距离就变成C-1了,这是又要将C分为奇数,偶数进行讨论。
那么是否存在N是奇数且C是偶数的情况呢,
假设从出发位置到进环的位置相差L,slow进环时,fast已经走了x圈,且fast与slow相差N:
进环时:slow走的距离->L
fast走的距离->L+x*C+C-N
fast的距离应该为slow的三倍:3*L=L+x*C+C-N
化简为:2*L=(x+1)*C-N 若要满足该等式,若C是偶数,N必须是偶数。若N是奇数,如果C是偶数,则(x+1)*偶数一定是偶数,偶数-奇数!=偶数。
所以上述条件不成立,故永远追不上的条件不成立。
结论:一定能追上。
N是偶数第一轮追上。N是奇数第一轮追不上,C是奇数,第二轮追上。
其他走四步等的条件证明过程类似。
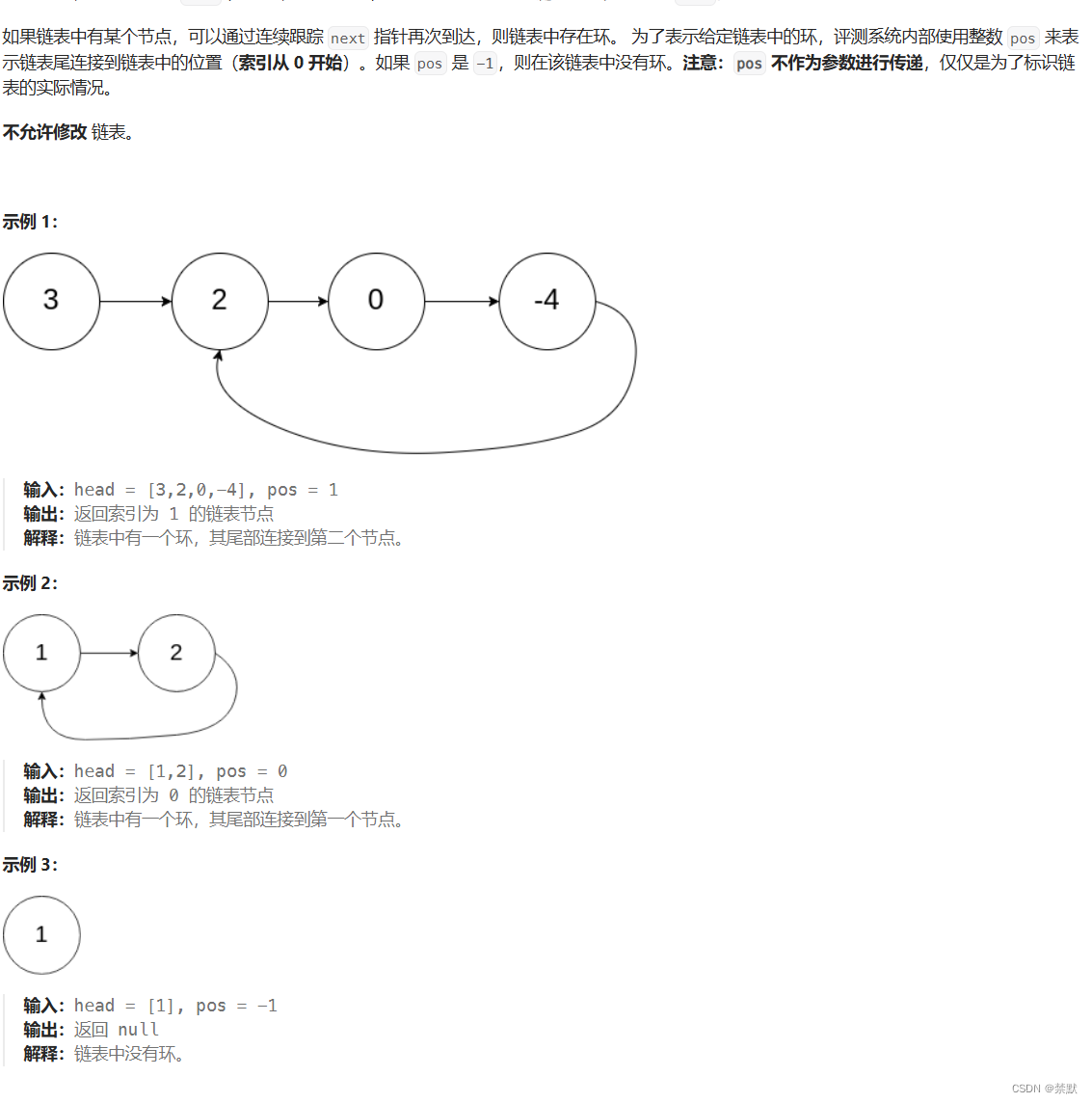
环形链表2
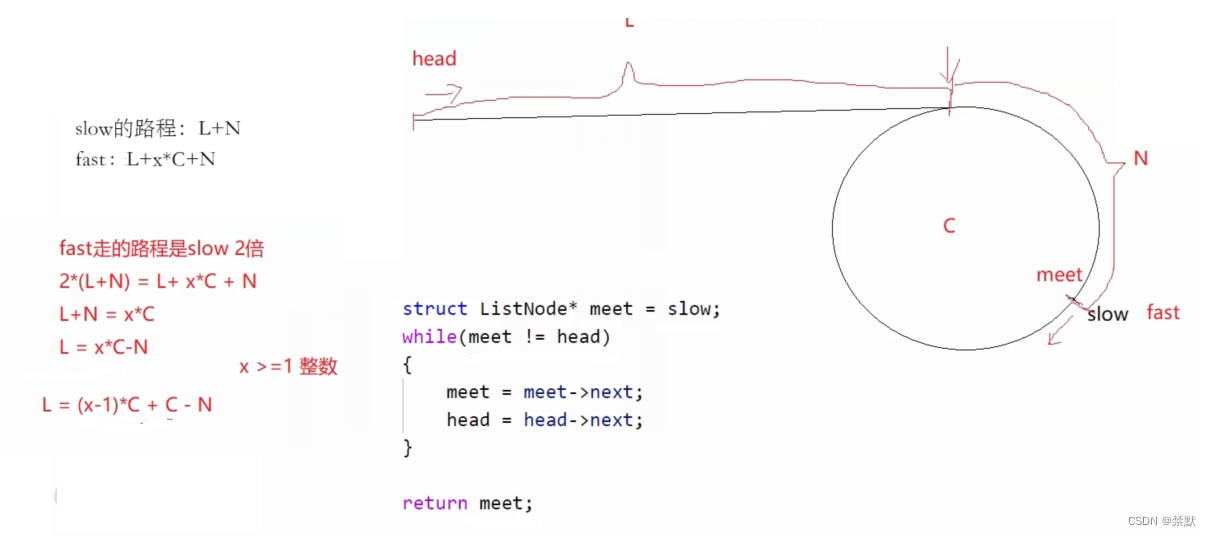
本题相较于第一个环形链表题,多了返回节点位置的步骤,所以最初思路也是通过快慢指针,快慢指针相遇,则证明有环存在,然后将两指针相遇点记为meet,再继续走,此时头节点也开始移动,meet与head相遇点就是环的最初节点。
证明过程如下:
struct ListNode {
int val;
struct ListNode *next;
};
typedef struct ListNode LN;
struct ListNode *detectCycle(struct ListNode *head) {
LN*slow,*fast,*meet;
slow=fast=head;
while(fast && fast->next){
slow=slow->next;
fast=fast->next->next;
if(slow==fast){
meet=slow;
while(meet!=head){
meet=meet->next;
head=head->next;
}
return meet;
}
}
return NULL;
}
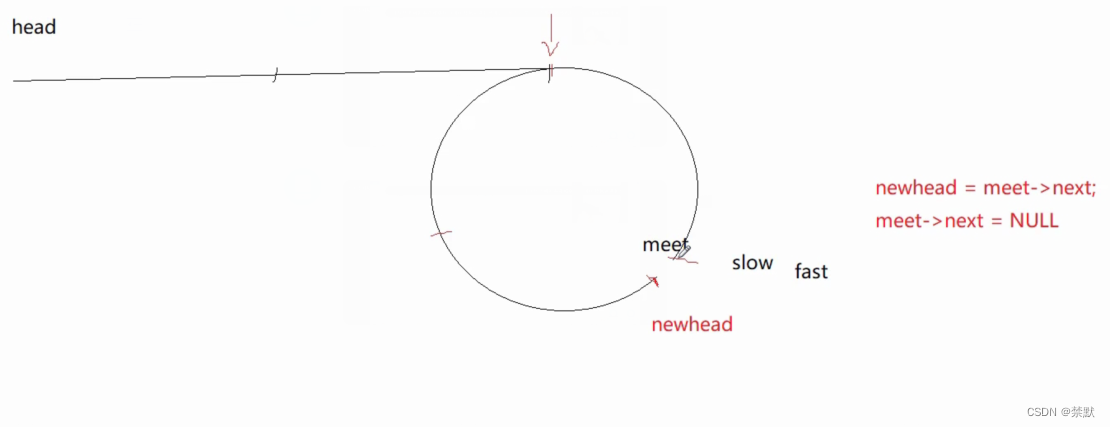
这种方法不容易想到,还有另外一种方法,将快慢指针相遇点newhead=meet->next,meet->next=NULL,此时从newhead开始,与原链表head通过相交链表的思路求解。
struct ListNode {
int val;
struct ListNode *next;
};
typedef struct ListNode LN;
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
LN*cur1=headA,*cur2=headB;
int lenA=1,lenB=1;
while(cur1){
cur1=cur1->next;
lenA++;
}
while(cur2){
cur2=cur2->next;
lenB++;
}
//尾节点不相同就没有相交
if(cur1!=cur2){
return NULL;
}
//假设法
int gap=abs(lenA-lenB);
LN* longlist = headA;
LN* shortlist = headB;
if(lenAnext;
}
while(longlist!=shortlist){
longlist=longlist->next;
shortlist=shortlist->next;
}
return longlist;
}
struct ListNode *detectCycle(struct ListNode *head) {
LN*slow,*fast,*meet;
slow=fast=head;
while(fast && fast->next){
slow=slow->next;
fast=fast->next->next;
if(slow==fast){
meet=slow;
LN* newhead=meet->next;
meet->next=NULL;
return getIntersectionNode(head,newhead);
}
}
return NULL;
}