【练习】分治--快排思想

目录

颜色分类

题目描述 

题解  

代码实现

排序数组

题目描述 

 题解

代码实现 

数组中的第k个最大元素

题目描述 

 题解

​编辑 代码实现

库存管理III( 最小k个数)

题目描述 

​编辑 题解

代码实现 

                                                   分治：分而治之. 

颜色分类

题目描述 

题解  

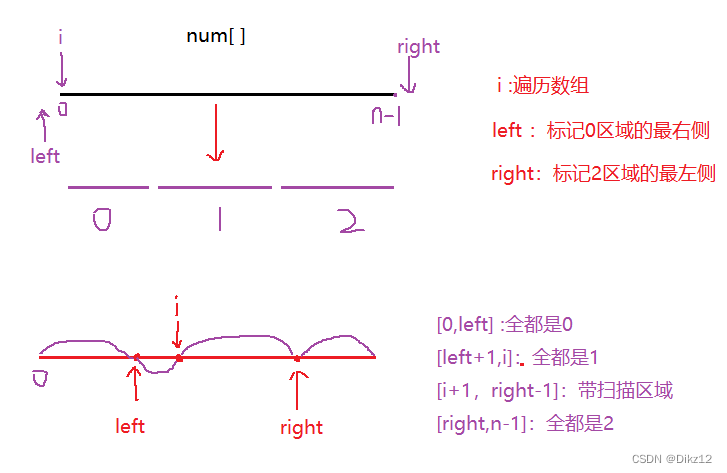
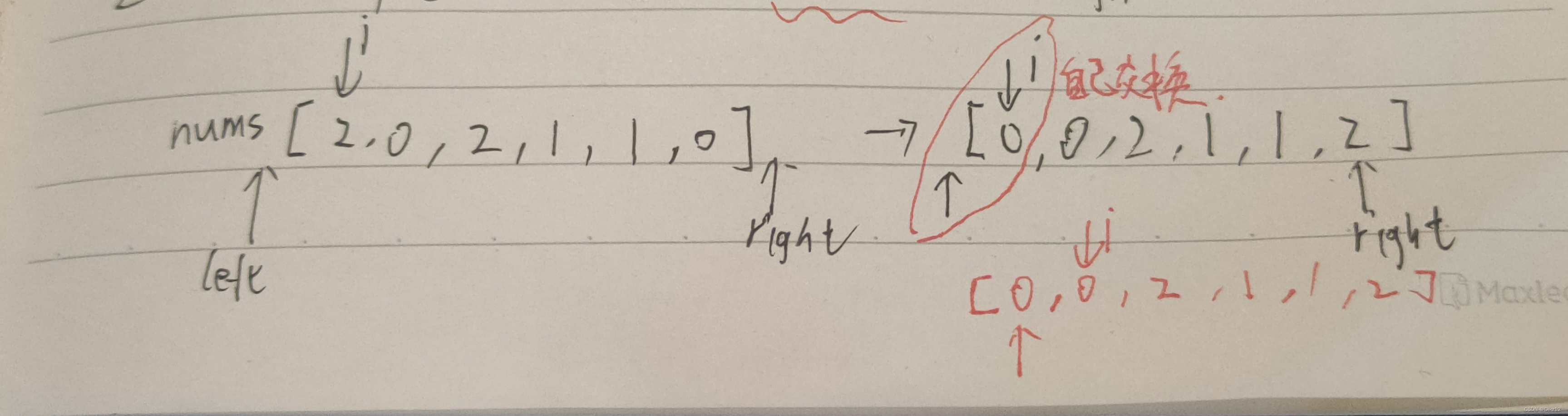
 解法：三指针（数组分三块）.

代码实现

    public void sortColors(int[] nums) {
        int i = 0, left = -1, right = nums.length;
        while(i  
排序数组
 
题目描述 
 
 
 题解
 
 解法：快速排序（数组分三块+随机选择基准）.
 
 
  
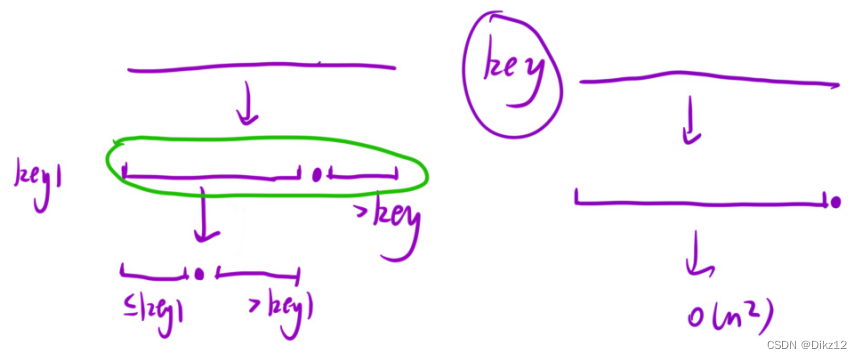
  快排最核⼼的⼀步就是 Partition (分割数 据)：将数据按照⼀个标准，分成左右两部分。 
  
 
   这里 
  不是使用的是将数组分成两部分（挖坑法、Hoare法）。 
  
 
 
  
  而是使⽤荷兰国旗问题的思想，将数组划分为 左 中 右 三部分：左边是⽐基准元素⼩的数据， 中间是与基准元素相同的数据，右边是⽐基准元素⼤的数据。然后再去递归的排序左边部分和右边 部分即可（可以舍去⼤量的中间部分）。  
  
  
  在处理数据量有很多重复的情况下，效率会⼤⼤提升！！！ 
  
 
数组分三块，过程就跟上题一样就不在进行详述.
 
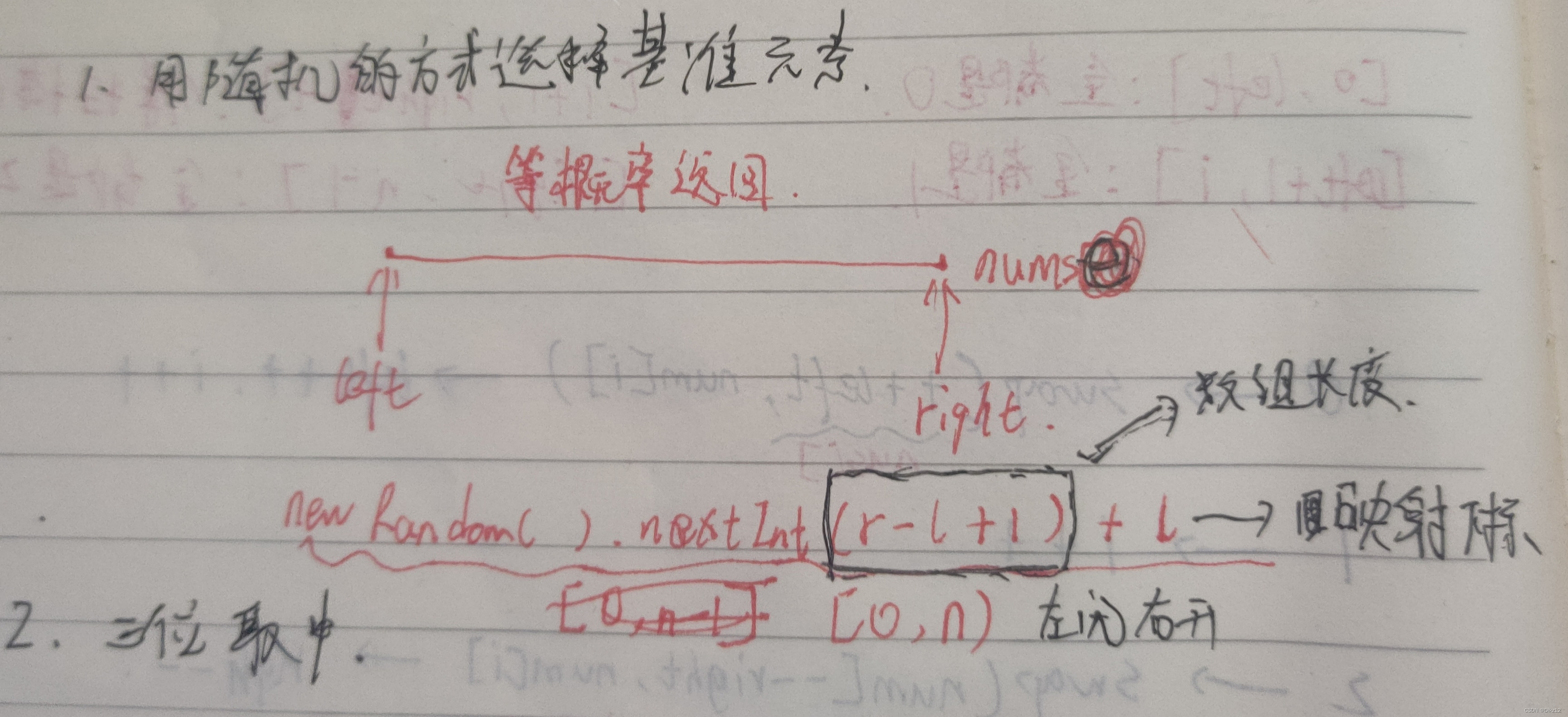
优化方式有：随机选择基准 和 三位取中.
 
 
 
代码实现 
 
    public int[] sortArray(int[] nums) {
        qsort(nums,0,nums.length - 1);
        return nums;
    }
    public void qsort(int[] nums,int l , int r) {
        //递归结束
        if (l >= r) {
            return;
        }
        //数组分三块
        int key = nums[new Random().nextInt(r - l + 1) + l];
        int left = l - 1, i = l, right = r + 1;
        while(i  
 挖坑法、Hoare法+优化：
 
 数组分三块+优化
 
 
数组中的第k个最大元素
 
题目描述 
 
 
 
 题解
 
解法：快速选择算法（数组分三块+随机选取基准元素） 。
 
 
  
  在快排中，当我们把数组「分成三块」之后：  
  [l, left] [left + 1, right - 1]  
  
  
  [right, r]  
  ，我们可以通过计算每⼀个区间内元素的「个数」，进⽽推断出我们要找的元素是  
  
  
  在「哪⼀个区间」⾥⾯。 那么我们可以直接去「相应的区间」去寻找最终结果就好了。 
  
 
 代码实现
 
    public int findKthLargest(int[] nums, int k) {
        return qsort(nums,0,nums.length-1,k);
    }
    public int qsort(int[] nums,int l ,int r, int k) {
        //结束条件
        if (l >= r) {
            return nums[l];
        }
        //1.随机选取基准
        int key = nums[new Random().nextInt(r - l + 1) + l];
        //2.数组分"三块"
        int i = l , left = l - 1, right = r + 1;
        while(i = k) {
            return qsort(nums,right,r,k);
        } else if (b + c >= k) {
            return key;
        } else {
            return qsort(nums,l,left,k - c - b);
        }
    }
    public void swap(int[] nums, int i , int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }
 
库存管理III( 最小k个数)
 
题目描述 
 
 题解
 
解法一：堆排.（大根堆）O(NlogN).
 
解法二：快速选择算法（数组分三块+随机选取基准元素） O(N) 
 
 
 在快排中，当我们把数组「分成三块」之后：  
 [l, left] [left + 1, right - 1]  
 
 
 [right, r]  
 ，我们可以通过计算每⼀个区间内元素的「个数」，进⽽推断出最⼩的 k 个数在哪  
 
 
 些区间⾥⾯。 那么我们可以直接去「相应的区间」继续划分数组即可。  
 
 
 
代码实现 
 
    public int[] inventoryManagement(int[] nums, int cnt) {
        qsort(nums,0,nums.length-1,cnt);
        int[] ret = new int[cnt];
        for(int i = 0; i = r) {
            return;
        }
        //1.随机选取基准
        int key = nums[new Random().nextInt(r - l + 1) + l];
        //2.数组分三块
        int i = l, left = l - 1,right = r + 1;
        while(i = k) {
            qsort(nums,l,left,k);
        } else if(a + b >= k) {
            return;
        } else {
            qsort(nums,right,r,k - a - b);
        }
    }
    public void swap(int[] nums, int i , int j) {
        int tmp = nums[i];
        nums[i] = nums[j];
        nums[j] = tmp;
    }