【C++学习】哈希的应用—位图与布隆过滤器
目录
- 1.位图
- 1.1位图的概念
- 1.2位图的实现
- 3.位图的应用
- 2.布隆过滤器
- 2.1 布隆过滤器提出
- 2.2布隆过滤器概念
- 2.3如何选择哈希函数个数和布隆过滤器长度
- 2.4布隆过滤器的实现
- 2.4.1布隆过滤器插入操作
- 2.4.2布隆过滤器查找操作
- 2.4.3 布隆过滤器删除
- 2.5 布隆过滤器优点
- 2.6布隆过滤器缺陷
- 3.海量数据面试题
- 3.1 哈希切割
- 3.2 位图应用
- 3.3 布隆过滤器
文章简介:
在这篇文章中,你会学习到关于哈希思想的最常见的两个应用,也就是 位图 与 布隆过滤器,
文章会讲解位图和布隆过滤器的概念,底层实现,对应的适应的场景,以及相关经典 海量数据面试题 及解析。
1.位图
1.1位图的概念
所谓位图,就是用每一位来存放某种状态,适用于海量数据,数据无重复的场景。通常是用来判断某个数据存不存在的。
比如这道 腾讯 的面试题目:
面试题目:给40亿个不重复的无符号整数,没排过序。给一个无符号整数,如何快速判断一个数是否在这40亿个数中。
解析:
40亿个整型数据所需内存大小:10亿字节约等于1G,那么40亿个整型,就是40亿*4(字节)=160亿字节≈16G。
- 遍历,时间复杂度O(N)
- 排序(O(NlogN)),利用二分查找: logN
上面的两种做法都是不可行的,因为内存不够。
- 位图解决 数据是否在给定的整形数据中,结果是在或者不在,刚好是两种状态,那么可以使用一个二进制比特位(0/1)来代表数据是否存在的信息,如果二进制比特位为1,代表存在,为0代表不存在。
第三种方法,利用位图解决,因为是要在40亿个数中查找,数据的类型是一个整型,范围为0~UINT_MAX。所以我们只需要UINT_MAX个比特位,所需的内存也就是512M,然后将这40亿个整数利用这UINT_MAX个比特位就可以表示他们的存在状态;
图解:
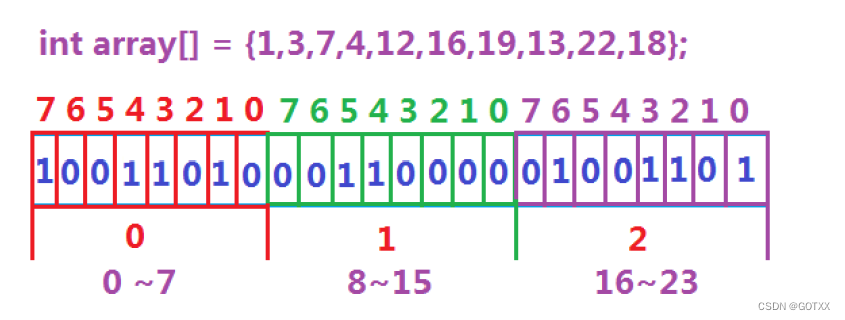
假设有一个整型数组array(如下图),因为里面的数据范围为1~22,所以我们就可以开一个int大小的数组(有32个比特位,可以表示32个不同数的存在状态),映射地址的方法这里采用的是直接定址法;
计算:第i个整型中:i = (该数)/ 32;
该整形中第j个比特位:j = (该数)% 32;
1.2位图的实现
-
因为位图需要整型的连续的空间,所以这里我们用vactor 即可
-
所开空间的大小的计算:
这里开的是一个范围,假如上面的面试题,有40亿个整型数据,因为有40亿个数据,但是不能 只开40亿个比特位的空间,因为如果只开了40亿个比特位的话,就只能表示数据大小为0~40亿的数据,然而数据类型为int,数据最大值超过了40亿,这样超过了40亿的数据就表示不了了。
-
因为空间开的大小不一样,所以这里需要利用非类型模板参数
-
所开的空间是以整型为单位开辟,所以确认了所需的比特位后,还需计算是多少个int(32个比特位)大小,如果换算为int大小,有余数的话,就应该多开一个int大小
template //非类型模板参数 class bitset { public: bitset() { _bitset.resize(N/32+1, 0); //所需开的空间,因为空间都只能以整型为单位开,所以需要除以32 } void set(size_t x) //将x对应的比特位置1 { size_t i = x / 32; //确定是第几个int size_t j = x % 32; //确定是该int里面的第几个比特位 _bitset[i] |= (1 size_t i = x / 32; size_t j = x % 32; _bitset[i] &= ~(1 size_t i = x / 32; size_t j = x % 32; return _bitset[i] & (1 size_t operator()(const string& s) { size_t hash = 0; for (auto ch : s) { hash *= 131; hash += ch; } return hash; } }; struct Func2 { size_t operator()(const string& s) { size_t hash = 0; for (size_t i = 0; i