最强总结，用Python实现十大回归算法！【文末IT资源分享】

2024-07-12 1358阅读

目录

1. 线性回归 (Linear Regression)

原理

核心公式

Python实现

2. 岭回归 (Ridge Regression)

原理

核心公式

Python实现

3. lasso回归 (Lasso Regression)

原理

核心公式

Python实现

4. 弹性网络回归 (Elastic Net Regression)

原理

核心公式

Python实现

5. 多项式回归 (Polynomial Regression)

原理

核心公式

Python实现

6. 支持向量回归 (Support Vector Regression, SVR)

原理

核心公式

Python实现

7. 决策树回归 (Decision Tree Regression)

原理

核心公式

Python实现

8. 随机森林回归 (Random Forest Regression)

原理

核心公式

Python实现

9. 梯度提升回归 (Gradient Boosting Regression)

原理

核心公式

Python实现

10. 贝叶斯回归 (Bayesian Regression)

原理

核心公式

Python实现

最后

福利：包含：Java、云原生、GO语音、嵌入式、Linux、物联网、AI人工智能、python、C/C++/C#、软件测试、网络安全、Web前端、网页、大数据、Android大模型多线程、JVM、Spring、MySQL、Redis、Dubbo、中间件…等最全厂牌最新视频教程+源码+软件包+面试必考题和答案详解。福利：想要的资料全都有 ，全免费，没有魔法和套路————————————————

拉到文末，有学习资源分享

今天咱们把回归类算法对应的原理和Python案例都详细的给大家说说，希望可以帮助到大家~

回归算法是机器学习中解决预测问题的核心方法，广泛应用于金融、医疗、市场营销等领域。它们通过建立变量之间的关系模型，能够有效地预测连续型目标变量，为决策提供数据支持。通过不同的正则化和集成技术，回归算法可以提高模型的准确性和稳定性，解决过拟合、欠拟合等问题。

今天还是围绕这十种最常见、最重要的回归类算法展开！~

  • 线性回归

  • 岭回归

  • 拉索回归

  • 弹性网络回归

  • 多项式回归

  • 支持向量回归

  • 决策树回归

  • 随机森林回归

  • 梯度提升回归

  • 贝叶斯回归

    下面给出了每种算法的详细介绍、原理、核心公式和推导，以及对应的Python案例~

    1. 线性回归 (Linear Regression)

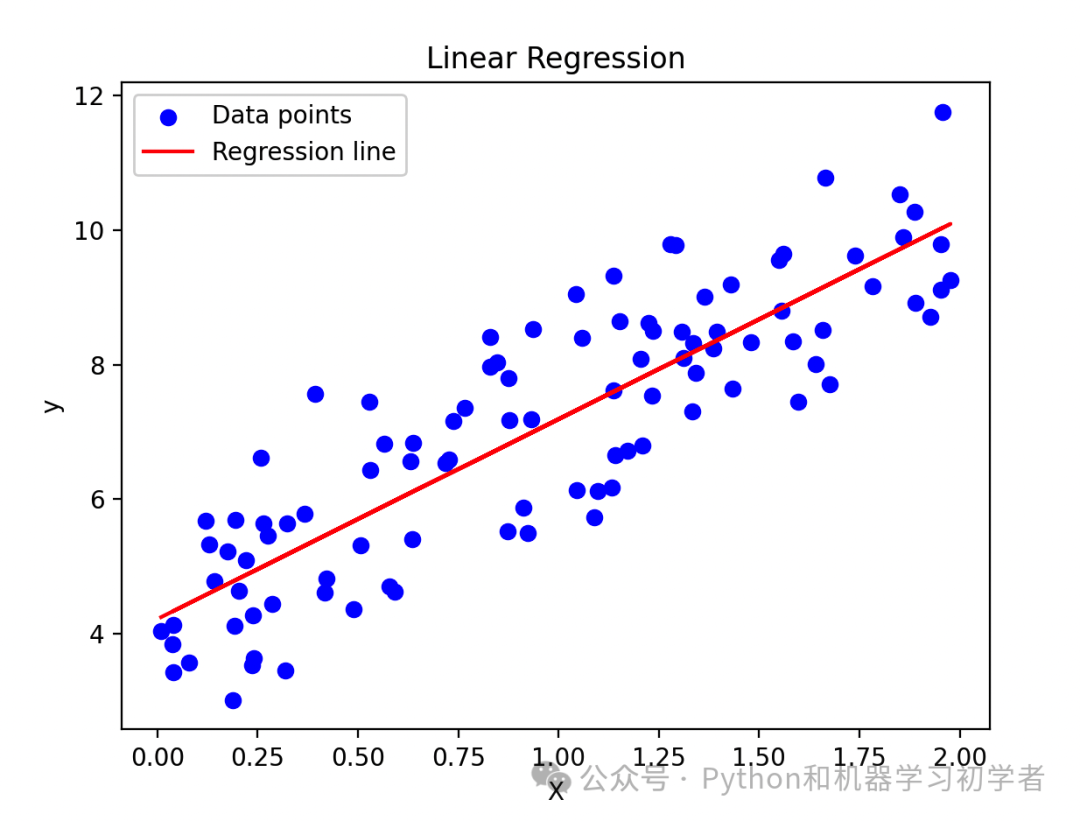
    线性回归是一种用于建模因变量和一个或多个自变量之间关系的统计方法。它假设自变量和因变量之间存在线性关系。

    原理

    线性回归的目标是找到最佳拟合的直线，使得样本数据点到该直线的距离（误差平方和）最小。

    核心公式

    线性回归模型的公式为：

    其中， 是因变量， 是自变量， 是截距， 是斜率， 是误差项。

    线性回归通过最小化误差平方和（Sum of Squared Errors, SSE）来估计参数  和 ：

    对  和  求偏导数，并设为零，得到一组线性方程，通过解这个方程组可以得到最优的  和 。

    Python实现

    import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成随机数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 线性回归模型
lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_pred = lin_reg.predict(X)
# 绘图
plt.scatter(X, y, color='blue', label='Data points')
plt.plot(X, y_pred, color='red', label='Regression line')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Linear Regression')
plt.legend()
plt.show()

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

    2. 岭回归 (Ridge Regression)

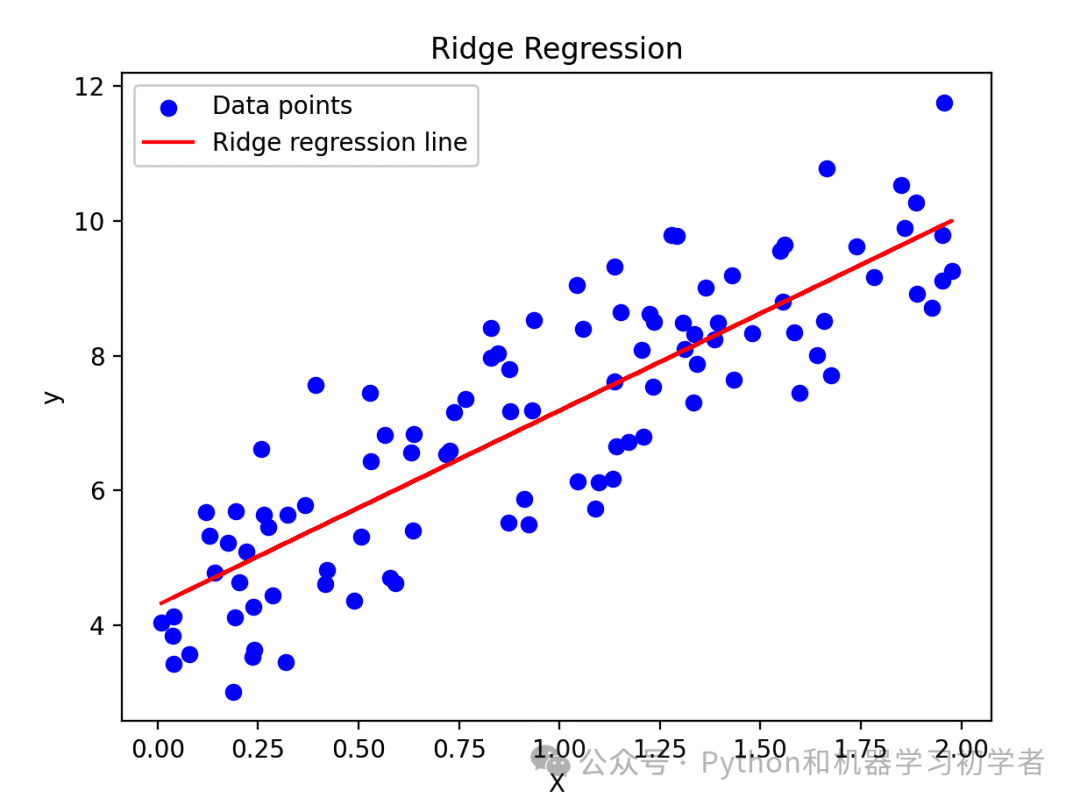
    岭回归是一种用于处理多重共线性问题的回归方法。通过在最小二乘法中加入L2正则化项，可以防止模型的过拟合。

    原理

    岭回归在最小化误差平方和的基础上加入了一个正则化项，目的是惩罚模型参数的大小，防止过拟合。

    核心公式

    岭回归的目标是最小化以下损失函数：

    其中， 是正则化参数，控制正则化项的影响。

    岭回归的损失函数为：

    通过对  求导并设为零，可以得到岭回归的解析解：

    Python实现

    import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
# 生成随机数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 岭回归模型
ridge_reg = Ridge(alpha=1, solver="cholesky")
ridge_reg.fit(X, y)
y_pred = ridge_reg.predict(X)
# 绘图
plt.scatter(X, y, color='blue', label='Data points')
plt.plot(X, y_pred, color='red', label='Ridge regression line')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Ridge Regression')
plt.legend()
plt.show()

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

    3. lasso回归 (Lasso Regression)

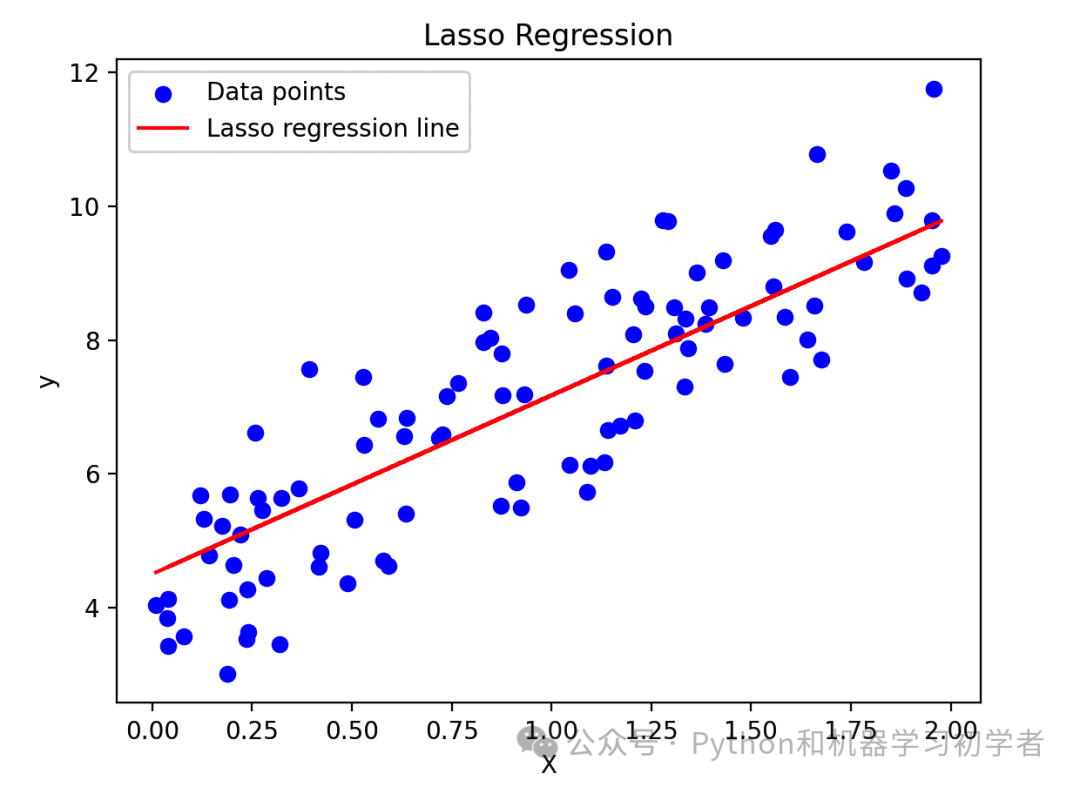
    拉索回归通过在最小二乘法中加入L1正则化项来减少过拟合，并且能够产生稀疏模型，即某些系数会被压缩为零，这有助于特征选择。

    原理

    拉索回归在最小化误差平方和的基础上加入了一个L1正则化项，以控制模型的复杂度。

    核心公式

    拉索回归的目标是最小化以下损失函数：

    其中， 是正则化参数，控制正则化项的影响。

    拉索回归的损失函数为：

    由于L1正则化项的非光滑性，拉索回归的解析解较难求解，通常使用坐标轴下降法等数值优化方法进行求解。

    Python实现

    import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
# 生成随机数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 拉索回归模型
lasso_reg = Lasso(alpha=0.1)
lasso_reg.fit(X, y)
y_pred = lasso_reg.predict(X)
# 绘图
plt.scatter(X, y, color='blue', label='Data points')
plt.plot(X, y_pred, color='red', label='Lasso regression line')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Lasso Regression')
plt.legend()
plt.show()

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

    4. 弹性网络回归 (Elastic Net Regression)

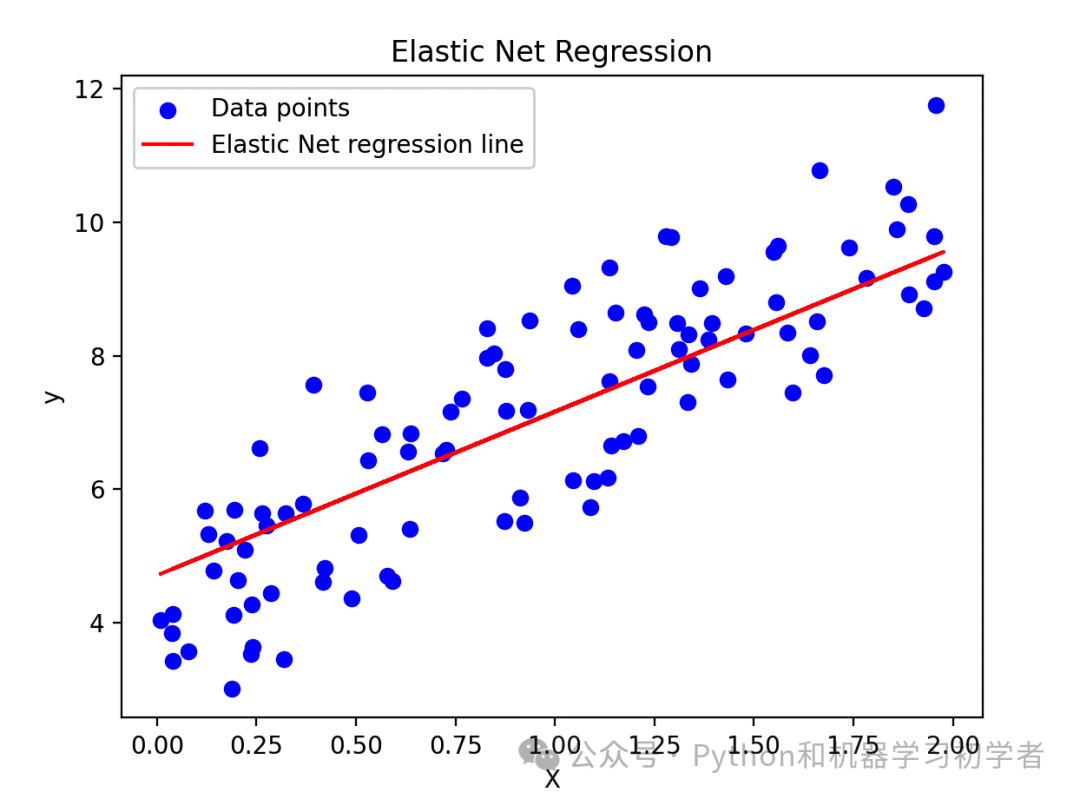
    弹性网络回归结合了岭回归和拉索回归的优点，通过同时引入L1和L2正则化项，适用于高维数据和多重共线性问题。

    原理

    弹性网络回归在最小化误差平方和的基础上同时加入L1和L2正则化项，以控制模型的复杂度并增强特征选择能力。

    核心公式

    弹性网络回归的目标是最小化以下损失函数：

    其中， 和  是正则化参数，控制L1和L2正则化项的影响。

    弹性网络回归的损失函数为：

    由于包含L1和L2正则化项，弹性网络回归的解析解较难求解，通常使用数值优化方法进行求解。

    Python实现

    import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet
# 生成随机数据
np.random.seed(0)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
# 弹性网络回归模型
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
y_pred = elastic_net.predict(X)
# 绘图
plt.scatter(X, y, color='blue', label='Data points')
plt.plot(X, y_pred, color='red', label='Elastic Net regression line')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Elastic Net Regression')
plt.legend()
plt.show()

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

    5. 多项式回归 (Polynomial Regression)

    多项式回归是一种扩展线性回归的方法，通过将特征进行多项式变换，可以捕捉到自变量和因变量之间的非线性关系。

    原理

    多项式回归将自变量通过多项式变换（例如二次方、三次方等）扩展，然后在变换后的特征上进行线性回归。

    核心公式

    多项式回归模型的公式为：

    其中， 是因变量， 是自变量， 是模型参数， 是误差项。

    多项式回归的推导与线性回归类似，只是特征向量  经过多项式变换：

    然后使用最小二乘法来估计参数 。

    Python实现

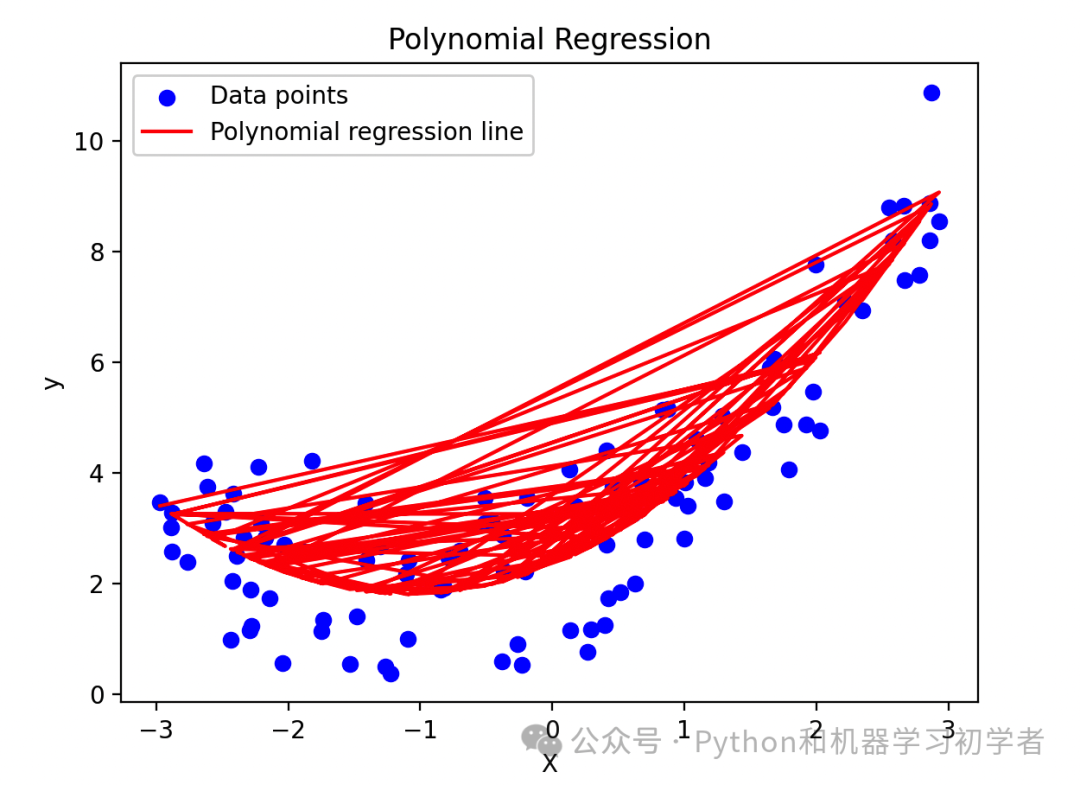
    import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
# 生成随机数据
np.random.seed(0)
X = 6 * np.random.rand(100, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(100, 1)
# 多项式特征变换
poly_features = PolynomialFeatures(degree=2, include_bias=False)
X_poly = poly_features.fit_transform(X)
# 线性回归模型
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)
y_pred = lin_reg.predict(X_poly)
# 绘图
plt.scatter(X, y, color='blue', label='Data points')
plt.plot(X, y_pred, color='red', label='Polynomial regression line')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Polynomial Regression')
plt.legend()
plt.show()

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

    6. 支持向量回归 (Support Vector Regression, SVR)

    支持向量回归是一种基于支持向量机的回归方法，适用于高维空间中的非线性回归问题。

    原理

    SVR的目标是找到一个能够以最大间隔包含大多数数据点的回归超平面，同时允许少量数据点在该间隔外。

    核心公式

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

    Python实现

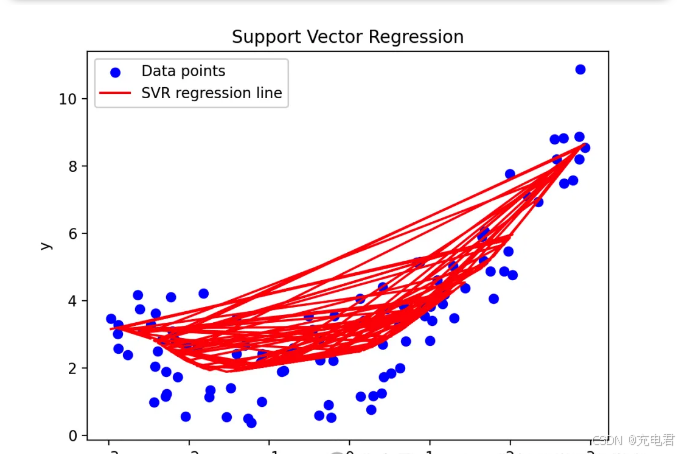
    import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVR
# 生成随机数据
np.random.seed(0)
X = 6 * np.random.rand(100, 1) - 3
y = 0.5 * X**2 + X + 2 + np.random.randn(100, 1)
# 支持向量回归模型
svr = SVR(kernel='rbf', C=100, epsilon=0.1)
svr.fit(X, y.ravel())
y_pred = svr.predict(X)
# 绘图
plt.scatter(X, y, color='blue', label='Data points')
plt.plot(X, y_pred, color='red', label='SVR regression line')
plt.xlabel('X')
plt.ylabel('y')
plt.title('Support Vector Regression')
plt.legend()
plt.show()

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

    7. 决策树回归 (Decision Tree Regression)

    决策树回归是一种基于树状结构的回归方法，通过递归地将数据集划分成更小的子集来进行预测。

    原理

    决策树回归的目标是通过递归地选择特征和切分点，将数据集划分成尽可能纯的子集，并在叶节点上预测目标值。

    核心公式

    决策树回归通过最小化以下损失函数来选择最佳特征和切分点：

    其中， 是第  个叶节点的样本集， 是第  个叶节点的预测值。

    决策树回归通过递归地选择特征和切分点，将数据集划分成尽可能纯的子集，并在叶节点上预测目标值。这个过程可以使用CART（分类和回归树）算法来实现。

    Python实现

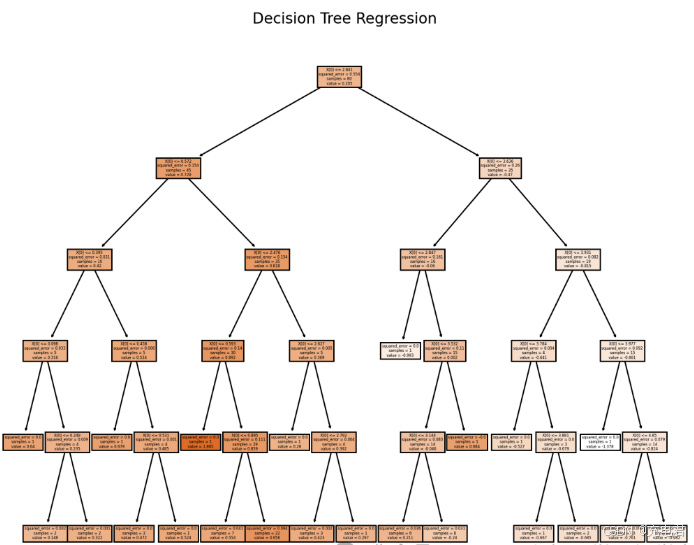
    # 导入所需的库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor, plot_tree
# 创建一个虚拟数据集
np.random.seed(0)
X = np.sort(5 * np.random.rand(80, 1), axis=0)
y = np.sin(X).ravel()
y[::5] += 3 * (0.5 - np.random.rand(16))  # 添加噪声
# 训练回归模型
regressor = DecisionTreeRegressor(max_depth=5)
regressor.fit(X, y)
# 绘制决策树图像
plt.figure(figsize=(10, 8))
plot_tree(regressor, filled=True)
plt.title("Decision Tree Regression")
plt.show()

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

    8. 随机森林回归 (Random Forest Regression)

    随机森林回归是一种基于集成学习的回归方法，通过集成多棵决策树来提高预测准确性和鲁棒性，减少过拟合。

    原理

    随机森林回归通过构建多个决策树并取其平均预测值来进行预测，每棵决策树在训练时使用随机的特征子集和样本子集。

    核心公式

    随机森林回归的预测值为：

    其中， 是第  棵决策树的预测值， 是决策树的数量。

    随机森林回归通过以下步骤来构建模型：

    1. 对于每棵决策树，从原始数据集中随机采样（有放回）得到训练集。

    2. 在训练每棵决策树时，随机选择特征的子集来决定最佳分裂。

    3. 集成所有决策树的预测结果。

    Python实现

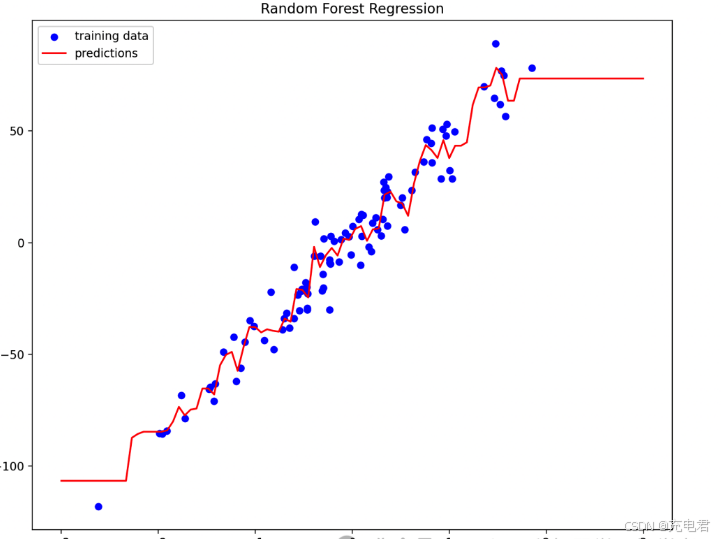
    import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_regression
from sklearn.ensemble import RandomForestRegressor
X, y = make_regression(n_samples=100, n_features=1, noise=10, random_state=42)
# 训练随机森林回归模型
regressor = RandomForestRegressor(n_estimators=100, random_state=42)
regressor.fit(X, y)
# 预测结果
X_test = np.linspace(-3, 3, 100).reshape(-1, 1)
y_pred = regressor.predict(X_test)
# 绘制随机森林中的一棵决策树图像
estimator = regressor.estimators_[0]
plt.figure(figsize=(10, 8))
plt.scatter(X, y, color="b", s=30, marker="o", label="training data")
plt.plot(X_test, y_pred, color="r", label="predictions")
plt.title("Random Forest Regression")
plt.xlabel("Feature")
plt.ylabel("Target")
plt.legend(loc="upper left")
# 可视化一棵决策树
plt.figure(figsize=(15, 10))
from sklearn.tree import plot_tree
plot_tree(estimator, filled=True, feature_names=['Feature'])
plt.title("Example Decision Tree from Random Forest")
plt.show()

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

    9. 梯度提升回归 (Gradient Boosting Regression)

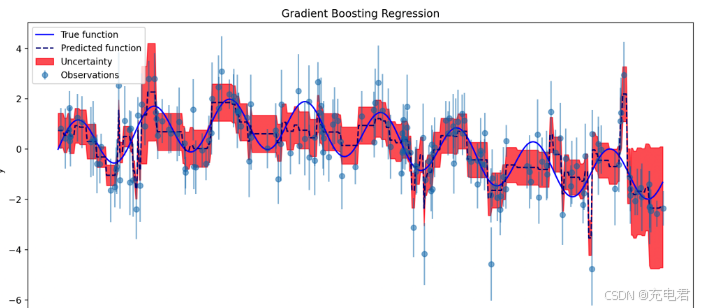
    梯度提升回归通过逐步构建一系列弱学习器（如决策树）来提升模型性能，适用于处理复杂的非线性关系。

    原理

    梯度提升回归通过逐步添加新的弱学习器来拟合前一个模型的残差，从而不断减少预测误差。

    核心公式

    梯度提升回归的预测值为：

    其中， 是第  个弱学习器的预测值， 是其权重， 是弱学习器的数量。

    梯度提升回归通过以下步骤来构建模型：

    1. 初始化模型，使用一个常数预测值。

    2. 迭代地训练弱学习器，拟合前一个模型的残差。

    3. 更新模型，将弱学习器的预测值加权后添加到当前模型中。

    Python实现

    import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
# 创建一个非线性函数作为模拟数据
def true_function(x):
    return np.sin(x) + np.sin(10 * x)
# 生成模拟数据
np.random.seed(0)
X = np.sort(5 * np.random.rand(200, 1), axis=0)
y = true_function(X).ravel()
dy = 0.5 + 1.0 * np.random.rand(200)
y += np.random.normal(0, dy)
# 拟合梯度提升回归模型
est = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1,
                                max_depth=3, random_state=0, loss='ls')
est.fit(X, y)
# 生成预测数据
X_test = np.arange(0.0, 5.0, 0.01)[:, np.newaxis]
y_pred = est.predict(X_test)
# 绘制结果
plt.figure(figsize=(10, 6))
plt.errorbar(X.ravel(), y, dy, fmt='o', alpha=0.5, label='Observations')
plt.plot(X_test, true_function(X_test), label='True function', color='blue')
plt.plot(X_test, y_pred, '--', color='navy', label='Predicted function')
plt.fill_between(X_test.ravel(), y_pred - est.estimators_[0][0].predict(X_test), y_pred + est.estimators_[0][0].predict(X_test), color='red', alpha=0.6, label='Uncertainty')
plt.title('Gradient Boosting Regression')
plt.legend(loc='upper left')
plt.xlabel('X')
plt.ylabel('y')
plt.show()

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

    10. 贝叶斯回归 (Bayesian Regression)

    贝叶斯回归是一种基于贝叶斯统计理论的回归方法，通过引入先验分布来进行参数估计，适用于小样本和不确定性较大的数据。

    原理

    贝叶斯回归通过结合先验分布和似然函数，利用贝叶斯公式进行参数估计，得到后验分布。

    核心公式

    贝叶斯回归的贝叶斯公式为：

    其中， 是后验分布， 是似然函数， 是先验分布， 是边际似然。

    贝叶斯回归通过以下步骤来估计参数：

    1. 选择适当的先验分布 。

    2. 计算似然函数 。

    3. 利用贝叶斯公式计算后验分布 。

    Python实现

    import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import BayesianRidge
# 创建一个非线性函数作为模拟数据
def true_function(x):
    return np.sin(x) + np.sin(2 * x) + np.sin(3 * x)
# 生成模拟数据
np.random.seed(0)
X = np.sort(5 * np.random.rand(200, 1), axis=0)
y = true_function(X).ravel()
dy = 0.5 + 1.0 * np.random.rand(200)
y += np.random.normal(0, dy)
# 贝叶斯线性回归模型
poly = PolynomialFeatures(degree=5)
X_poly = poly.fit_transform(X)
clf = BayesianRidge(compute_score=True)
clf.fit(X_poly, y)
# 生成预测数据
X_test = np.linspace(0, 5, 100)[:, np.newaxis]
y_pred, y_std = clf.predict(poly.transform(X_test), return_std=True)
# 绘制结果
plt.figure(figsize=(10, 6))
plt.errorbar(X.ravel(), y, dy, fmt='o', alpha=0.5, label='Observations')
plt.plot(X_test, true_function(X_test), color='green', label='True function')
plt.plot(X_test, y_pred, '--', color='navy', label='Predicted function')
plt.fill_between(X_test.ravel(), y_pred - y_std, y_pred + y_std, color='red', alpha=0.6, label='Uncertainty')
plt.title('Bayesian Regression with Polynomial Features')
plt.legend(loc='upper left')
plt.xlabel('X')
plt.ylabel('y')
plt.show()

    最后

    以上就是今天所有的内容了。

    如果对你来说比较有用，记得点赞、收藏，慢慢学习~

    下期会有更多干货等着你！~

    福利：

    包含：Java、云原生、GO语音、嵌入式、Linux、物联网、AI人工智能、python、C/C++/C#、软件测试、网络安全、Web前端、网页、大数据、Android大模型多线程、JVM、Spring、MySQL、Redis、Dubbo、中间件…等最全厂牌最新视频教程+源码+软件包+面试必考题和答案详解。

    福利：想要的资料全都有 ，全免费，没有魔法和套路

    ————————————————

       

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

    关注公众号：资源充电吧

    点击小卡片关注下，回复：学习

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

    最强总结，用Python实现十大回归算法！【文末IT资源分享】

VPS购买请点击我

免责声明：我们致力于保护作者版权，注重分享，被刊用文章因无法核实真实出处，未能及时与作者取得联系，或有版权异议的，请联系管理员，我们会立即处理! 部分文章是来自自研大数据AI进行生成,内容摘自(百度百科,百度知道,头条百科,中国民法典,刑法,牛津词典,新华词典,汉语词典,国家院校,科普平台)等数据,内容仅供学习参考,不准确地方联系删除处理! 图片声明：本站部分配图来自人工智能系统AI生成,觅知网授权图片,PxHere摄影无版权图库和百度，360，搜狗等多加搜索引擎自动关键词搜索配图，如有侵权的图片，请第一时间联系我们，邮箱：ciyunidc@ciyunshuju.com。本站只作为美观性配图使用,无任何非法侵犯第三方意图,一切解释权归图片著作权方,本站不承担任何责任。如有恶意碰瓷者,必当奉陪到底严惩不贷!

相关阅读

目录[+]