BM42：混合搜索的新基准 - Qdrant

在过去的 40 年里，BM25 一直是搜索引擎的标准。它是一种简单但功能强大的算法，已被许多搜索引擎使用，包括 Google、Bing 和 Yahoo。

虽然看起来向量搜索的出现会削弱其影响力，但效果并不明显。目前最先进的检索方法试图将 BM25 与嵌入结合到混合搜索系统中。

然而，自从引入 RAG 以来，文本检索的使用情况发生了显著变化。BM25 所基于的许多假设不再有效。

例如，传统网络搜索和现代 RAG 系统之间文档和查询的典型长度存在很大差异。

在本文中，我们将回顾 BM25 为何如此受关注，以及为什么其他替代方法难以取代它。最后，我们将讨论 BM42，这是词汇搜索演进的下一步。

为何 BM25 能持续这么长时间？

要了解原因，我们需要分析其组成部分。

著名的BM25公式定义为：

score ⁡ ( D , Q ) = ∑ i = 1 N IDF ⁡ ( q i ) × f ( q i , D ) ⋅ ( k 1 + 1 ) f ( q i , D ) + k 1 ⋅ ( 1 − b + b ⋅ ∣ D ∣  avgdl  ) \operatorname{score}(D, Q)=\sum_{i=1}^N \operatorname{IDF}\left(q_i\right) \times \frac{f\left(q_i, D\right) \cdot\left(k_1+1\right)}{f\left(q_i, D\right)+k_1 \cdot\left(1-b+b \cdot \frac{|D|}{\text { avgdl }}\right)} score(D,Q)=i=1∑N​IDF(qi​)×f(qi​,D)+k1​⋅(1−b+b⋅ avgdl ∣D∣​)f(qi​,D)⋅(k1​+1)​

让我们简化这一点以便更好地理解。

• 这score(D,Q)-- 意味着我们计算每对文档的分数并查询。

• 这 ∑ i = 1 N \sum_{i=1}^N ∑i=1N​意味着每个查询中的术语将作为总和的一部分计入最终得分。

• 这 IDF ⁡ ( q i ) \operatorname{IDF}\left(q_i\right) IDF(qi​) 是逆文档频率。术语越罕见，越大，对得分的贡献就越大。简化的公式如下：

  IDF ⁡ ( q i ) =  Number of documents   Number of documents with  q i \operatorname{IDF}\left(q_i\right)=\frac{\text { Number of documents }}{\text { Number of documents with } q_i} IDF(qi​)= Number of documents with qi​ Number of documents ​

  可以说 是IDFBM25 公式中最重要的部分。 IDF选择查询中相对于特定文档集合最重要的术语。 因此直观地，我们可以将 解释为语料库中的术语IDF重要性。

  这解释了为什么 BM25 如此擅长处理查询，而密集嵌入认为这些查询超出了域范围。

  公式的最后一个部分可以直观地解释为文档中的术语重要性。这可能看起来有点复杂，所以让我们分解一下。

   Term importance in document  ( q i ) = f ( q i , D ) ⋅ ( k 1 + 1 ) f ( q i , D ) + k 1 ⋅ ( 1 − b + b ⋅ ∣ D ∣  avgdl  ) \text { Term importance in document }\left(q_i\right)=\frac{f\left(q_i, D\right) \cdot\left(k_1+1\right)}{f\left(q_i, D\right)+k_1 \cdot\left(1-b+b \cdot \frac{|D|}{\text { avgdl }}\right)}  Term importance in document (qi​)=f(qi​,D)+k1​⋅(1−b+b⋅ avgdl ∣D∣​)f(qi​,D)⋅(k1​+1)​

  • 这 f ( q i , D ) f\left(q_i, D\right) f(qi​,D) 是该词的频率在文档中换句话说，该术语的次数出现在文档中。
  • 这 k 1 k1 k1和 b 1 b1 b1是 BM25 公式的超参数。在大多数实现中，它们是设置为的常量和这些常数定义了公式中词频和文档长度的相对含义。
  • 这 ∣ D ∣  avgdl  \frac{|D|}{\text { avgdl }}  avgdl ∣D∣​ 是文档的相对长度与语料库中的平均文档长度相比。这部分的直觉如下：如果在较小的文档中找到标记，则该标记对该文档而言就更有可能是重要的。

    文档中的 BM25 术语重要性是否适用于 RAG？

    我们可以看出，_文档中的术语重要性_很大程度上取决于文档中的统计数据。此外，如果文档足够长，统计数据会很好用。因此，它适合搜索网页、书籍、文章等。

    但是，它是否也适用于现代搜索应用程序（例如 RAG）？让我们拭目以待。

    RAG 中文档的典型长度比网络搜索的文档长度短得多。事实上，即使我们处理的是网页和文章，我们也更愿意将它们分成块，以便 a) 密集模型可以处理它们，并且 b) 我们可以精确地找到与查询相关的文档的确切部分

    因此，RAG 中的文档大小很小且固定。

    这实际上使得 BM25 公式的文档部分中的词重要性变得毫无用处。文档中的词频始终为 0 或 1，文档的相对长度始终为 1。

    因此，BM25 公式中唯一与 RAG 相关的部分是IDF。让我们看看如何利用它。

    为什么 SPLADE 并不总是答案

    在讨论我们的新方法之前，让我们先来研究一下 BM25 的当前最先进的替代方案 - SPLADE。

    SPLADE 背后的想法很有趣——如果我们让一个智能的、端到端训练的模型为我们生成文本的词袋表示会怎么样？它会将所有权重分配给标记，因此我们无需担心统计数据和超参数。然后，文档将表示为稀疏嵌入，其中每个标记都表示为稀疏向量的一个元素。

    而且它在学术基准测试中表现良好。许多论文报告称，SPLADE 在检索质量方面优于 BM25。然而，这种性能是有代价的。

    • 不合适的标记器：要将转换器整合到此任务中，SPLADE 模型需要使用标准转换器标记器。这些标记器不是为检索任务设计的。例如，如果单词不在（相当有限的）词汇表中，它将被拆分为子词或替换为标记[UNK]。这种行为对于语言建模很有效，但对于检索任务却完全是破坏性的。

    • 昂贵的标记扩展：为了补偿标记化问题，SPLADE 使用_标记扩展_技术。这意味着我们为查询中的每个标记生成一组类似的标记。这种方法存在一些问题：

      • 它在计算和内存上都很昂贵。我们需要为文档中的每个标记生成更多值，这会增加存储大小和检索时间。
      • 标记扩展何时停止并不总是很清楚。我们生成的标记越多，我们获得相关标记的可能性就越大。但同时，我们生成的标记越多，我们获得不相关结果的可能性就越大。
      • 标记扩展削弱了搜索的可解释性。我们无法说出文档中使用了哪些标记，哪些标记是由标记扩展生成的。

      • 领域和语言依赖性：SPLADE 模型是在特定语料库上训练的。这意味着它们并不总是可以推广到新的或罕见的领域。由于它们不使用语料库中的任何统计数据，因此它们无法在不进行微调的情况下适应新领域。

      • 推理时间：此外，目前可用的 SPLADE 模型相当大且速度很慢。它们通常需要 GPU 才能在合理的时间内进行推理。

        在 Qdrant，我们承认上述问题并正在寻找解决方案。我们的想法是结合两全其美的优势——BM25 的简单性和可解释性以及 transformer 的智能性，同时避免 SPLADE 的缺陷。

        这就是我们的想法。

        两全其美的

        如前所述，IDF是 BM25 公式中最重要的部分。事实上，它非常重要，因此我们决定将其计算构建到 Qdrant 引擎本身中。查看我们最新的发布说明。这种类型的分离允许对稀疏嵌入进行流式更新，同时保持IDF计算最新。

        至于公式的第二部分，_文档中的重要性一词_需要重新考虑。

        既然我们不能依赖文档内的统计数据，那么我们可以尝试使用文档的语义。而语义正是 Transformer 所擅长的。因此，我们只需要解决两个问题：

        • 如何从变压器中提取重要信息？
        • 如何避免标记化问题？

          你只需要关注

          Transformer 模型（即使是用于生成嵌入的模型）也会生成大量不同的输出。其中一些输出用于生成嵌入。

          其他用于解决其他类型的任务，例如分类、文本生成等。

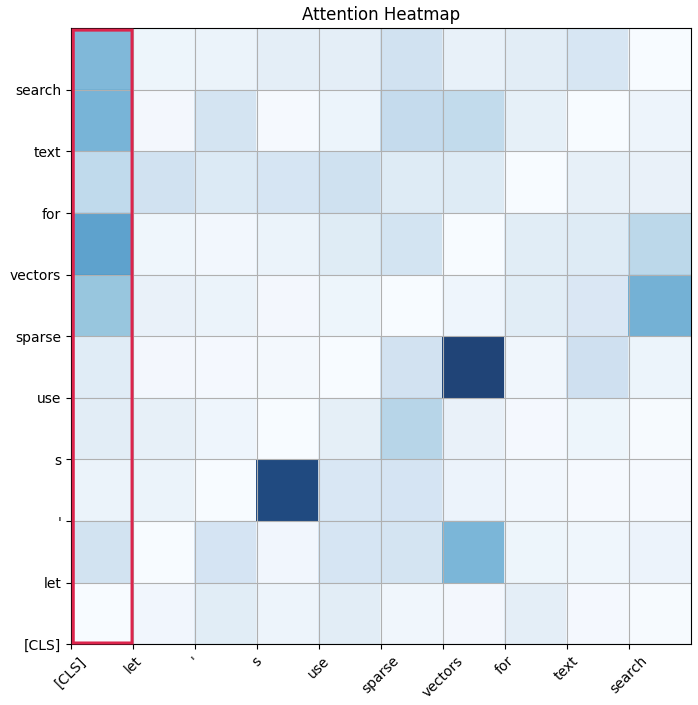
          对我们来说，一个特别有趣的输出是注意力矩阵。

          

          注意力矩阵

          注意力矩阵是一个方阵，每行每列对应输入序列中的token，表示输入序列中每个token对彼此的重要性。

          经典的 Transformer 模型经过训练可以预测上下文中的掩码标记，因此注意力权重定义了哪些上下文标记对掩码标记的影响最大。

          除了常规的文本 token，Transformer 模型还有一个名为 的特殊 token [CLS]。这个 token 代表了分类任务中的整个序列，这正是我们所需要的。

          通过查看[CLS]token 的注意力行，我们可以得到文档中每个 token 对整个文档的重要性。

          sentences = "Hello, World - is the starting point in most programming languages"
          features = transformer.tokenize(sentences)
          # ...
          attentions = transformer.auto_model(**features, output_attentions=True).attentions
          weights = torch.mean(attentions[-1][0,:,0], axis=0)                       
          #                ▲               ▲  ▲   ▲                                 
          #                │               │  │   └─── [CLS] token is the first one
          #                │               │  └─────── First item of the batch         
          #                │               └────────── Last transformer layer       
          #                └────────────────────────── Averate all 6 attention heads
          for weight, token in zip(weights, tokens):
              print(f"{token}: {weight}")
          # [CLS]       : 0.434 // Filter out the [CLS] token
          # hello       : 0.039
          # ,           : 0.039
          # world       : 0.107 //