Matlab实现最小二乘法的几种方法

        最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。

        按照图中所提出的问题（如图1），要求已知多组解（自变量和因变量），求出最佳和最恰当的参数的解，用数学建模的思路，这就是一个最小二乘法优化类问题

        最小二乘法拟合求解有线性拟合和非线性拟合，本文主要说明线性拟合部分。

一、线性最小二乘法拟合编程实现

        首先说明原理，对于最简单的线性函数模型：

        根据以上原理，编写代码，这里采用MATLAB编写，MATLAB具有强大的矩阵计算能力，还有线性拟合工具箱

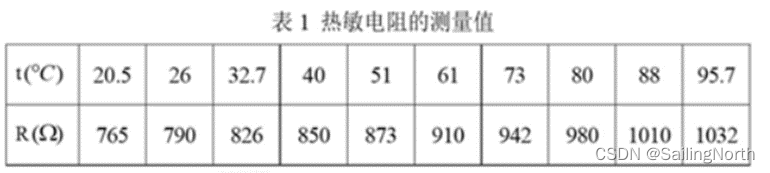
        为了方便得出结果，这里用一个热敏电阻的例子编程（压缩包中remingdianzu.m）

已知R=at+b

编写代码如下：

clear,clc;
t=[20.5,26,32.7,40,51,61,73,80,88,95.7];
R=[765,790,826,850,873,910,942,980,1010,1022];
figure;
plot(t,R,'*');
hold on
N=numel(t);
den=N*sum(t.^2)-sum(t)^2;
a=(sum(R)*sum(t.^2)-sum(R.*t)*sum(t))/den
b=(N*sum(R.*t)-sum(R)*sum(t))/den
t1=1:100;
R1=a+b*t1;
plot(t1,R1)
t=70
R2=a+b*t

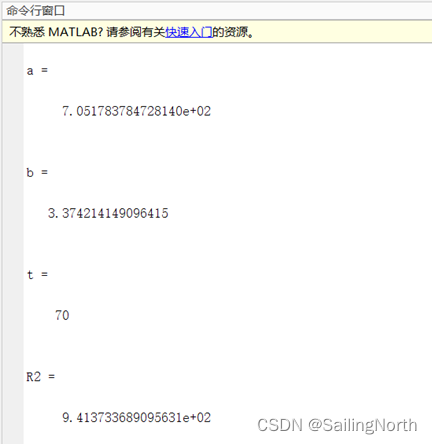
运行结果：

R2是带入t=70时求得的电阻值，可以看出比较合理。

二、cftool实现

        因为MATLAB具有一个最小二乘法线性拟合的工具箱，用它做最小二乘法拟合求参数十分方便。直接在命令行输入cftool。

cftool

        如下图所示窗口，只需要选择X data和Y data。在右侧的Degree中可以选择多项式的最高次数，如下图便是一次，红色部分圈起来的就是结果。

        改变次数可以求出不同的参数，如下图所示就是三次多项式的结果，使用起来十分方便，这里我不由得感叹MATLAB在数值方面的功能强大之处。