【C/排序算法】：归并排序和计数排序

目录

• 1. 归并排序
• 2. 计数排序

  1. 归并排序

  归并排序是一种效率仅次于快速排序的排序算法。它有非递归和递归两种实现方式(本文只讲述递归实现，非递归实现以后有专门的文章)。

  其实，归并排序也叫外排序。它不仅可以对内存中的数据进行排序，还能对文件里的数据排序。

  比如：假设有10G的数据放在硬盘的文件中，要排序，如何排呢？

  我们知道，内存里的空间远远没有10G，假设有1G内存可用。首先我们可以把10G的文件切分成10个1G的文件，再依次读文件，每次把1G的数据读入内存的数组中，接着利用快排对其进行排序，再把排好序的那1G的数据写到硬盘的一个文件，再继续读下一个1G的数据……当10个文件里的数据都分别有序时，再利用归并排序进行两两归并，最终使10G的数据有序。

  1.算法思想：

  归并排序采用分治法。首先假设一组数据的左半区间有序，右半区间有序，将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

  若将两个有序表合并成一个有序表，称为二路归并。

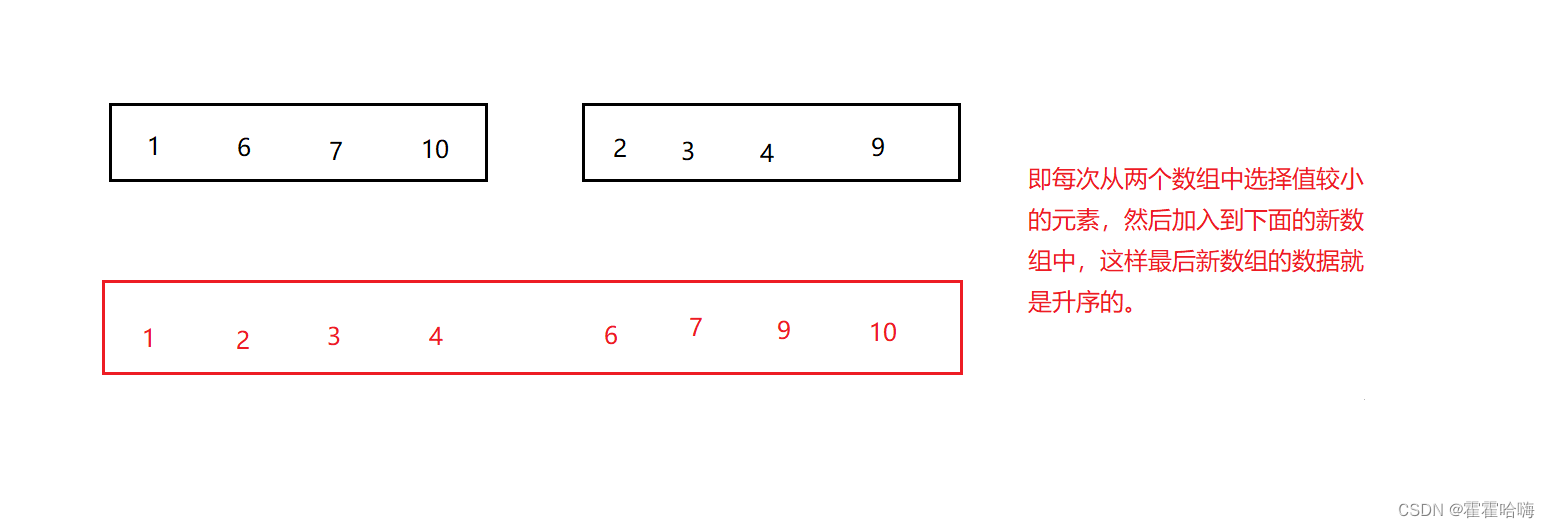
  所谓 归并，就是将两组有序的数据合成为一组有序的数据。 例如有如下两个有序数组，将两个有序数组归并为一个有序数组，这就是一次归并操作。

  

  2.归并操作的工作原理如下：

  第一步：申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列。

  第二步：设定两个指针，最初位置分别为两个已经排序序列的起始位置。

  第三步：比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置。

  重复步骤3直到某一指针超出序列尾，将另一序列剩下的所有元素直接复制到合并序列尾。

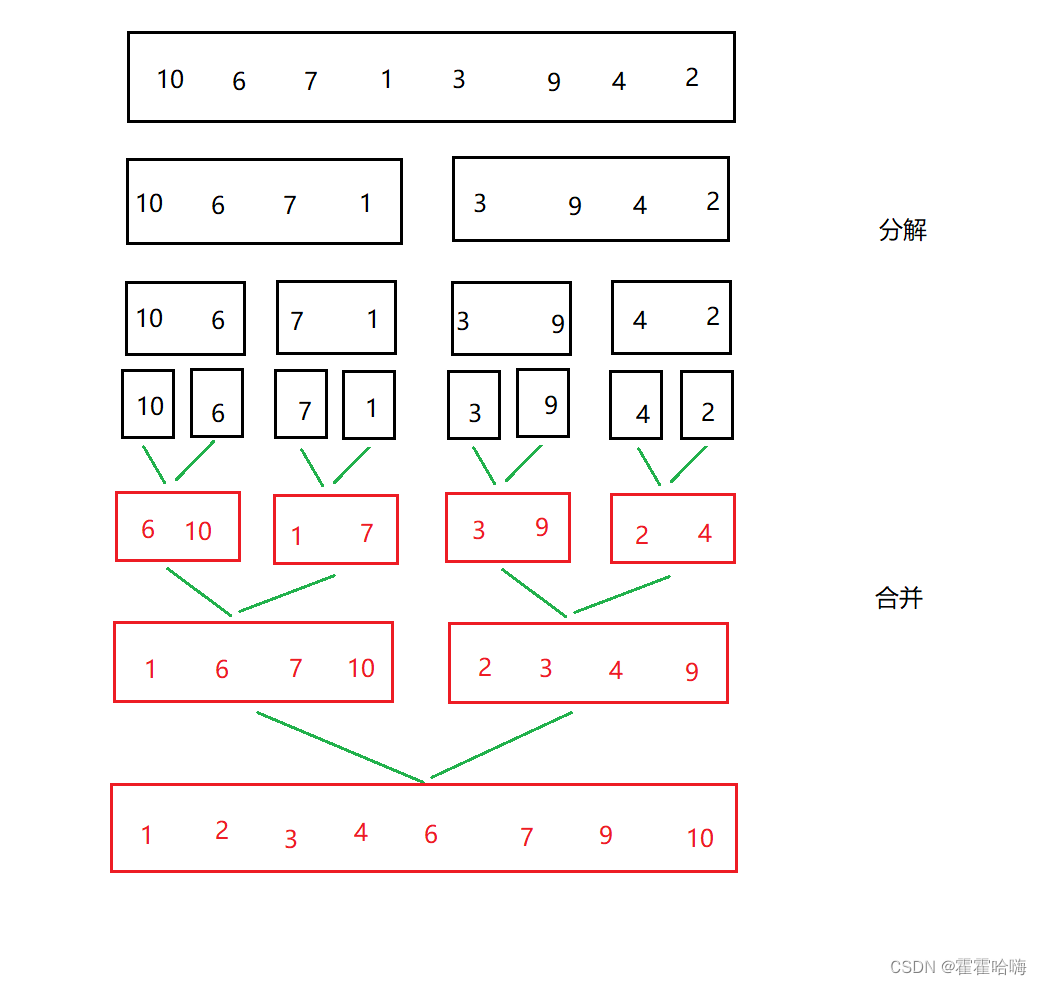
  归并排序类似于二叉树的后序遍历，即先将左右的区间都排为有序后，然后才开始进行归并操作，因为归并必须要满足两个数组是有序的。

  例如有如下数组。需要先将该数组每次都分割为两个区间，直到最后每个区间都只有一个值，此时比较两个值大小，然后将该两个值归并到一个数组中，此时就得到一个有两个元素的有序数组，然后再与另一个有两个元素的有序数组进行归并，然后就得到了一个有四个元素的有序数组，然后再与另一个有四个元素的有序数组进行归并，就得到了一个有八个元素的有序数组。就这样依次递归归并，直到最后目标数组为有序数组。

  

  3.归并排序的代码实现如下：

  //把数组分成区间
  void _MergrSort(int* arr,int left,int right,int* tmp)
  {
      //当区间内只有一个元素时，认为有序，递归结束，开始归并
  	if (left == right)
  		return ;
  		
       //右移1位右除以2的效果，用来把数组分成两个区间
  	int mid = (left + right) >> 1;
  	//假设[left mid] [mid+1 right]有序，就可以归并
  	_MergrSort(arr, left, mid, tmp);
  	_MergrSort(arr, mid + 1, right, tmp);
       //每次归并的过程
  	int begin1 = left;
  	int end1 = mid;
  	int begin2 = mid + 1;
  	int end2 = right;
  	
  	//注意：这里的index不要给0，因为在递归过程中left不一定等于0
  	int index = left;
  	
  	//有一个区间结束就停止
  	while (begin1 
  		if (arr[begin1] 
  			tmp[index++] = arr[begin1++];
  		}
  		else
  		{
  			tmp[index++] = arr[begin2++];
  		}
  	}
  	//当其中有一个区间结束时，另一个有序区间的数据直接拷贝进临时数组里
  	while (begin1 
  		tmp[index++] = arr[begin1++];
  	}
  	while (begin2 
  		tmp[index++] = arr[begin2++];
  	}
  	//最后把临时数组里面的数据拷贝回原数组
  	//注意：这里拷贝时有可能是局部区间拷贝，要加 begin
  	memcpy(arr+begin, tmp+begin, sizeof(int) * (end -begin +1));
  }
  void MergrSort(int* arr, int sz)
  {
      //创建临时数组存放数据
  	int* tmp = (int*)malloc(sizeof(int) * sz);
  	if (tmp == NULL)
  	{
  		perror("malloc");
  		return;
  	}
  	
  	_MergrSort(arr, 0, sz - 1, tmp);
  	free(tmp);
  	tmp = NULL;
  }
  
  	int max = arr[0];
  	int min = arr[0];
  	//找出最大值和最小值
  	for (int i = 0; i