热词排序算法——贝叶斯均值法
热词排序算法——贝叶斯均值法
- 贝叶斯均值法
- 基本思想
- 假设变量
- 举例说明
- python实现
贝叶斯均值法
当前(例如今天)的某个词出现的频率相比于历史发生突增,那么这个词的热度上升。
当某个词历史出现的次数为0,而当前出现的次数为100,另一个词历史出现的频率为100,
今日出现的频率为200,虽然同增长100,但明显第一个词是0到1的一个增长,显然比第二个词更重要。
基本思想
- 假设所有案例都至少有m次曝光(设置一个基准),那么就都具备了同等的一个评选条件;
- 然后假设这m次曝光的评分是所有案例的平均得分(即假设这个案例具有平均水准) m v + m C \frac{m}{v+m}C v+mmC;
- 最后,用现有的评分进行修正,长期来看,v/(v+m)这部分的权重将越来越大,得分将慢慢接近真实情况。
W R = v v + m R + m v + m C WR = \frac{v}{v+m}R+\frac{m}{v+m}C WR=v+mvR+v+mmC
v : 代表该案例的实际观看量;
m : 代表最低的一个观看量(人工干预设置,可根据实际观看情况而定,平均值等等);
R : 该案例的平均得分;
C : 所有案例的平均得分。
假设变量
1、将单个词语的得分设置为 R ( w ) R(w) R(w)设置为 A t p ( w ) A t p ( w ) + B t p ( w ) = A t p ( w ) T p S u m ( w ) \frac{Atp(w)}{Atp(w)+Btp(w)}=\frac{Atp(w)}{TpSum(w)} Atp(w)+Btp(w)Atp(w)=TpSum(w)Atp(w)
在这里也可以采用牛顿冷却法设置得分值 N θ ( w ) = − l n 当前词频 历史词频 / 时间差 N_\theta(w) = -ln\frac{当前词频}{历史词频}/时间差 Nθ(w)=−ln历史词频当前词频/时间差
2、将人工干预设置设置为 m = a v g T p S u m ( w ) = T p A v g m =avg\ TpSum(w) = TpAvg m=avg TpSum(w)=TpAvg
3、将所有词元的平均得分设置为 C = a v g R ( w ) C=avg\ R(w) C=avg R(w)
则贝叶斯均值排名为:
W R = A t p ( w ) A t p ( w ) + T p A v g R ( w ) + T p A v g A t p ( w ) + T p A v g C WR=\frac{Atp(w)}{Atp(w)+TpAvg}R(w)+\frac{TpAvg}{Atp(w)+TpAvg}C WR=Atp(w)+TpAvgAtp(w)R(w)+Atp(w)+TpAvgTpAvgC
举例说明
词组 历史词频/Btp(w) 当前词频/Atp(w) 词频和/TpSum(w) 得分/R(w) WR 六合彩 1106 1702 2808 0.606 0.56385 修正 1106 100 1206 0.0829 0.45900 下横线 10 200 210 0.952 0.56848 线性回归 400 200 600 0.333 0.49580 无穷小 200 200 400 0.500 0.46902 TpAvg C Avg 1044.8 0.495 W R = A t p ( w ) A t p ( w ) + T p A v g R ( w ) + T p A v g A t p ( w ) + T p A v g C WR=\frac{Atp(w)}{Atp(w)+TpAvg}R(w)+\frac{TpAvg}{Atp(w)+TpAvg}C WR=Atp(w)+TpAvgAtp(w)R(w)+Atp(w)+TpAvgTpAvgC
python实现
新建一个测试集
from collections import Counter import pandas as pd test_df = pd.DataFrame( ( [["六合彩", "2024-01-20"] for i in range(1106)] + [["六合彩", "2024-01-21"] for i in range(1702)] + [["修正", "2024-01-20"] for i in range(1106)] + [["修正", "2024-01-21"] for i in range(100)] + [["下横线", "2024-01-20"] for i in range(10)] + [["下横线", "2024-01-21"] for i in range(200)] + [["线性回归", "2024-01-20"] for i in range(400)] + [["线性回归", "2024-01-21"] for i in range(200)] + [["无穷小", "2024-01-20"] for i in range(200)] + [["无穷小", "2024-01-21"] for i in range(200)] ) ) test_df编写算法
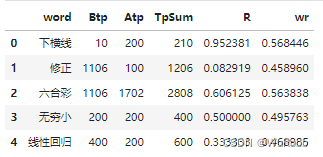
def bayes_avrage_rank(df: pd.DataFrame, base_time: str) -> pd.DataFrame: """ 贝叶斯平均法排名算法 :param df:初始数据格式为 [词元,时间] :param base_time: 设置分割时间 :return: 计算结果 """ columns = list(df.columns) conditions = df[columns[1]] > base_time # 在截止时间前后获取历史词元和当前词元计算Apt和Bpt apt = pd.DataFrame( Counter(df[conditions][columns[0]]).most_common(), columns=["word", "Atp"] ) bpt = pd.DataFrame( Counter(df[~conditions][columns[0]]).most_common(), columns=["word", "Btp"] ) df_pt = pd.merge(bpt, apt, how="outer", on="word") df_pt = df_pt.fillna(0) # 计算得分R(w) df_pt["TpSum"] = df_pt["Atp"] + df_pt["Btp"] df_pt["R"] = df_pt["Atp"] / df_pt["TpSum"] df_pt = df_pt.fillna(0) # 计算 m 和 C tp_avg = df_pt["TpSum"].mean() r_avg = df_pt["R"].mean() # 贝叶斯平均公式 wr = df_pt["Atp"] * df_pt["R"] / (df_pt["Atp"] + tp_avg) + tp_avg * r_avg / ( df_pt["Atp"] + tp_avg ) df_pt["wr"] = wr return df_pt bayes_avrage_rank(test_df, "2024-01-20")有兴趣可以自行替换牛顿冷却法。