【MATLAB】超前校正装置的设计

1.串联超前校正

        串联超前校正的实质是将超前网络的最大超前角补在校正后系统开环频率特性的截止频率处，提高校正后系统的相角裕度和截止频率，从而改善系统的动态性能。

        超前校正装置的传递函数可以写为：

 可见系统的开环增益会衰减到原来的1/a，所以需要串联一个放大器放大a倍，因此增益补偿后的校正装置传递函数为：

        只需要求出式子中的参数、，即可得到校正装置的传递函数。

2.超前校正的设计步骤

1. 根据稳态性能的要求，确定系统的开环增益 K 。
2. 根据确定后的开环增益K和原系统的传递函数，绘制出Bode图。
3. 在Bode图上求出原系统的相角裕度和幅值裕度，计算校正装置所应提供的超前相角  ,即,其中为期望的相角裕度，为原系统的相角裕度，是为了补偿因校正后截止频率增大导致的、校正前系统相角裕度的损失量，一般取~。
4. 再根据公式   求出校正装置参数，在Bode图上确定原系统幅值等于 dB对应的频率  。
5. 根据已经求出的和 ，将其值带入公式中，求出超前装置的参数和，并写出增益补偿后的校正装置传递函数。
6. 写出校正后系统的开环传递函数,并绘制校正后系统的Bode图，验证校正的结果。

3.超前校正仿真示例

        首先，在超前校正装置的设计中，会用到以下的函数：

函数	用法说明
bode(G)	绘制系统伯德图
[mag,phase,w]=bode(G)	返回系统伯德图相应的幅值、相位和频率向量
margin(G)	绘制系统伯德图，同时显示相位裕度、幅值裕度、截止频率和相角穿越频率
[gm,pm,wg,wc]=margin(G)	返回系统的幅值裕度、相位裕度、相角穿越频率和截止频率
feedback(sys1,sys2)	将系统sys1和sys2构成负反馈
spline(x0,y0,x)	三次样条插值，x0,y0是已知数据点，x是插值点，y是插值点的函数值。用于求原系统幅值等于 dB对应的频率  。
step(sys)	绘制系统sys的阶跃响应

         现在给出下面的例子，利用matlab设计一个超前校正装置。

        例：设被控对象的传递函数为：，设计要求：系统的速度误差系数为100，相角裕度不小于,试设计串联超前校正装置。

解  程序代码如下：

clear all;
close all;
%第一步，确定开环增益K
delta=6;%选Δφ为6°
k=100;%根据稳态条件确定系统的开环增益
ri=45;%期望相角裕度
%第二步，建立确定开环增益K后的系统的传递函数
num0=k;
den0=conv([0.001 1 0],[0.1 1]);
G0=tf(num0,den0);
%第三步，计算φm
[h,r]=margin(G0)%得到原系统的幅值裕度h和相角裕度r
phim=ri-r+delta;%计算φm
phim=phim*pi/180;%将φm转化为弧度制
%第四步，计算校正装置参数a和ωm
a=(1+sin(phim))/(1-sin(phim));%计算校正装置参数a的值
adb=10*log10(a);%将其a的单位转化为分贝
[mag,phase,w]=bode(G0);%得到系统的幅值、相位、角频率向量
magdb=20*log10(mag);%将幅值mag转化为分贝值
wm=spline(magdb,w,-adb);%计算出原系统幅值等于-10*lg(a)时的ωm
%第五步，计算校正装置参数T
T=1/(wm*sqrt(a));%计算根据a和ωm的值计算T的值
%第六步，得到校正装置的传递函数，绘制校正后的Bode图
Gc=tf([T*a 1],[T 1]);%得到增益补偿后的校正装置传递函数
[hc,rc]=margin(Gc*G0)%得到校正过后的系统的幅值裕度hc和相角裕量rc
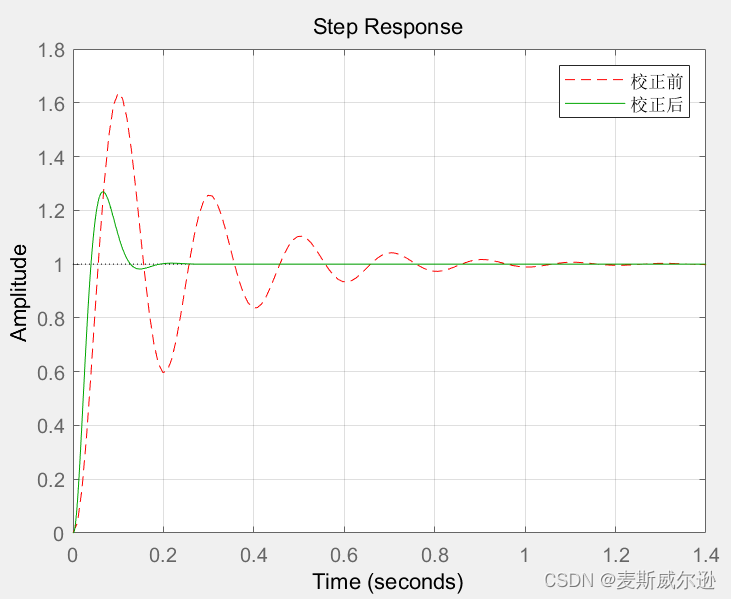
step(feedback(G0,1),'r--',feedback(Gc*G0,1),'g');grid on;%绘制系统校正前和校正后的阶跃响应
legend('校正前','校正后');
figure;bode(G0,Gc*G0);grid on;%绘制系统校正前和校正后的Bode图
legend('校正前','校正后');

运行结果如下：

r =
   16.2023
rc =
   45.3761

        可以看到，校正前系统的相角裕度为16.2°，校正后的系统相角裕度为45.4°，满足题目要求，说明设计的超前校正装置合理。系统校正前和校正后的阶跃响应和Bode图如下：

        通过上面的图形可以看出，校正后的相角裕度增加，提高了系统的稳定性；系统的截止频率右移，提高了系统的快速性。