数据结构 最小生成树 prim算法（普里姆算法）C语言实现

普里姆（prim）算法

• 一、定义
• 二、思路
• 三、代码实现
• 四、代码解析

  一、定义

  普里姆算法是一种构造性算法。假设G = (V， E)是一个具有n个顶点的带权连通图，T = (U，TE)是最小生成树，其中U是T的顶点集，TE是T的边集，则由G构造从起始点v出法的最小生成树T的步骤如下：

  1. 初始化U = { v }，以v到其他顶点的所有边为侯选边。
  2. 重复以下步骤(n - 1)次，使得其他(n - 1)个顶点被加入U中。

  （1）. 从候选边中挑选权值最小的边加入TE，设该边在V—U中的顶点是k，将k加入U中。

  （2）. 考察当前V—U中的所有顶点j，修改侯选边，若(k，j)的权值小于原来和顶点关联的侯选边，则用(k，j)取代后者作为侯选边。

  二、思路

  我们可以将定义理解为：将图的所有顶点分为两类，A类（保存已经查找过的顶点），B类（保存未查找过的顶点），从任一顶点开始，并将其从B类移至A类，然后开始寻找B类中（的顶点）到A类顶点之间权值最小的顶点，将其从B类中移至A类，重复上述操作，直至B类中没有顶点。所走过的顶点和边就是该连通图的最小生成树。

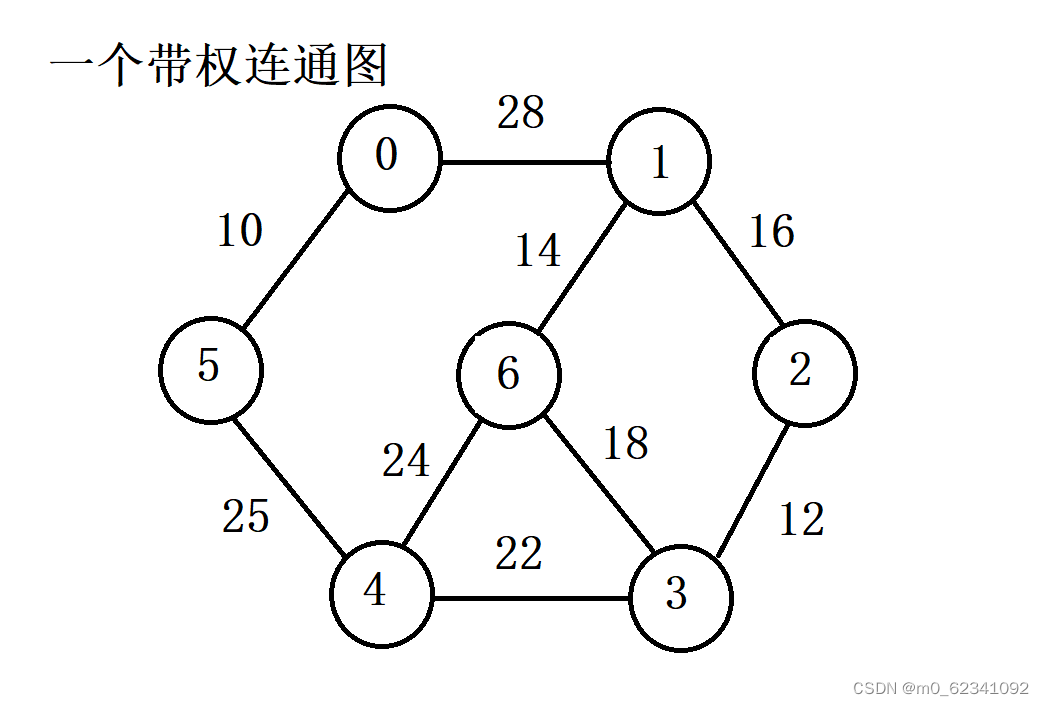
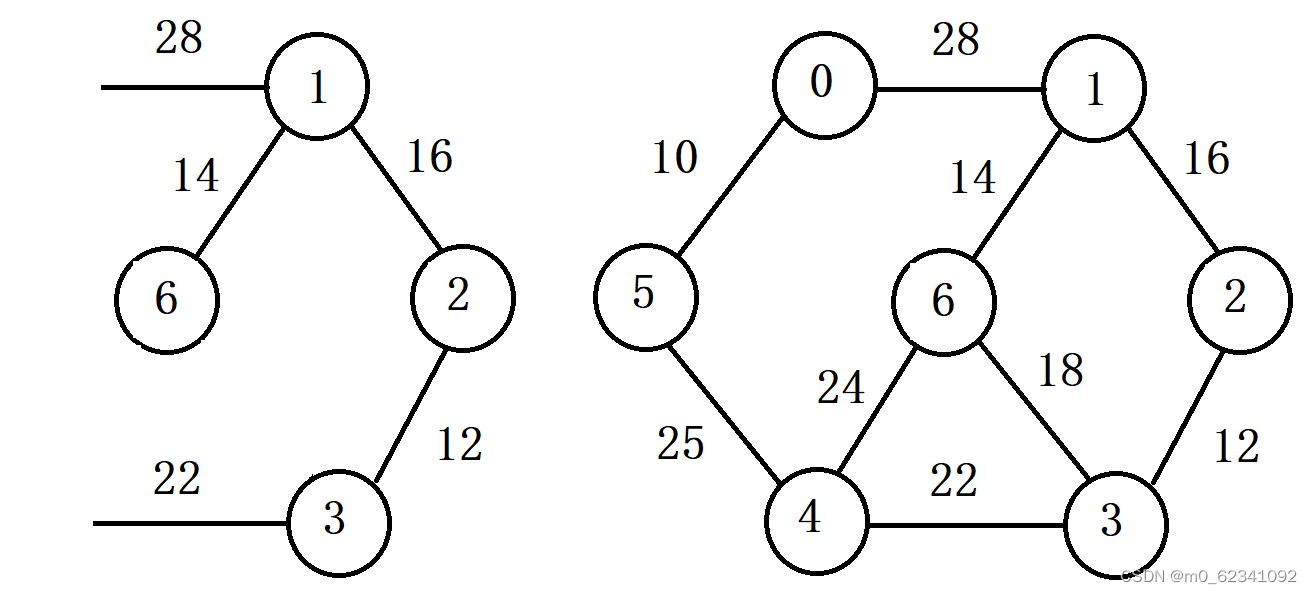
  由此图为例：

  

  初始状态

  A类 = { }

  B类 = { 0, 1, 2, 3, 4, 5, 6 }

  假设从顶点2开始遍历

  A类 = { 2 }

  B类 = { 0, 1, 3, 4, 5, 6 }

  遍历第一次后

  A类 = {2, 3 }

  B类 = { 0, 1, 4, 5, 6 }

  遍历第二次后

  A类 = { 1, 2, 3 }

  B类 = { 0, 4, 5, 6 }

  由此类推，直至B类中无顶点。

  A类 = { 0, 1, 2, 3, 4, 5, 6 }

  B类 = { }

  图型讲解如下：

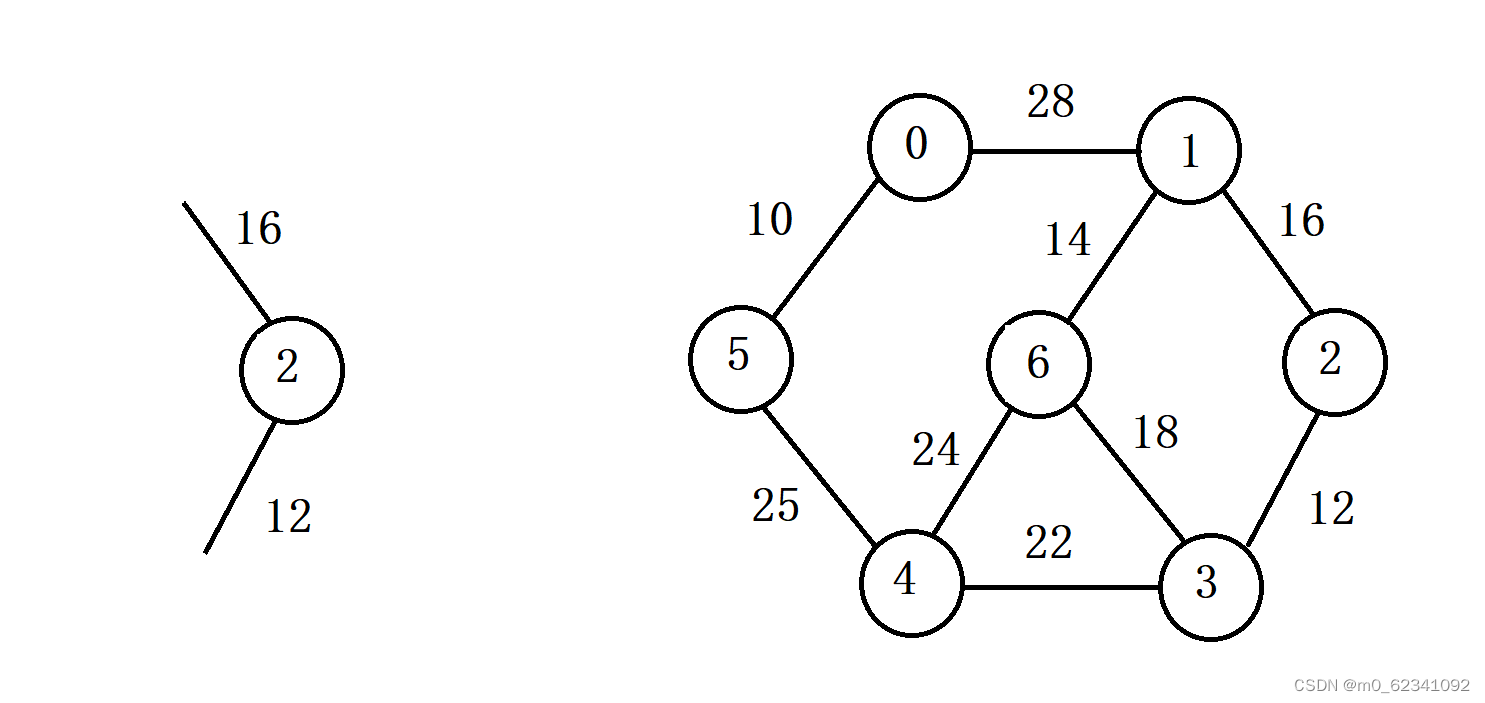
  假设从顶点2开始遍历。

  

  寻找B类到A类顶点之间权值最小的顶点（在现有的两条边寻找权值最小的边）。（上图为顶点3）将其添加至A类顶点中。

  

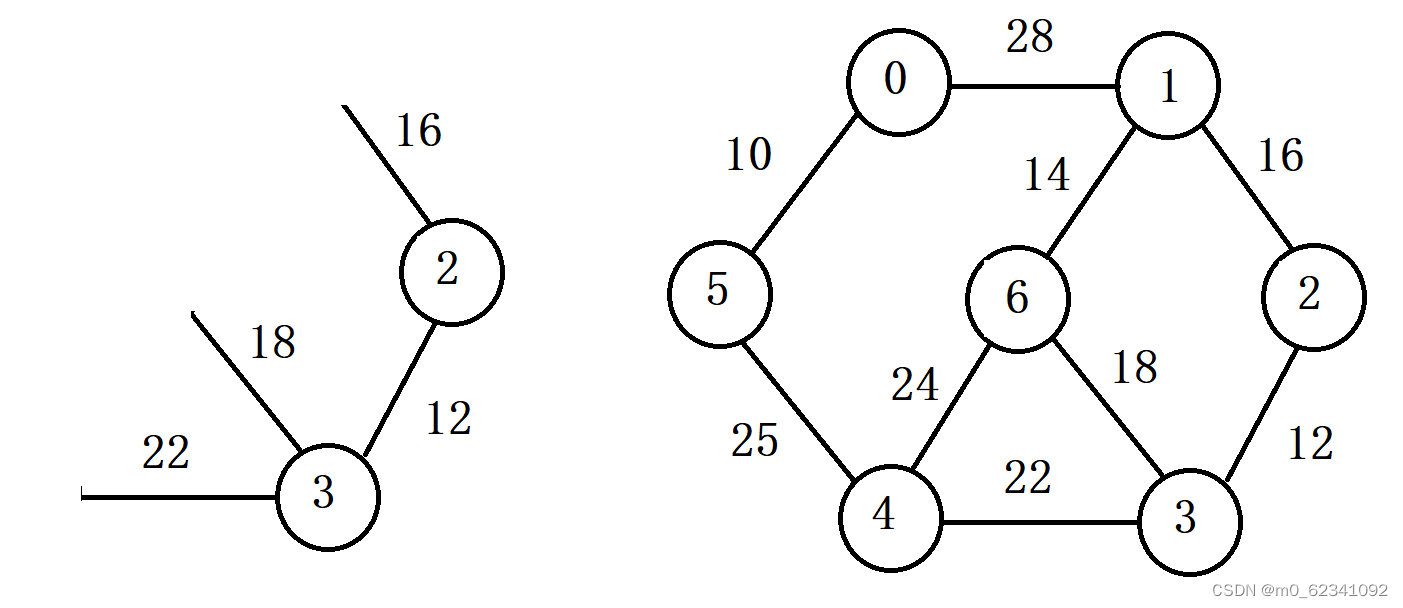
  步骤同上。在现有的三条边（权值为12的边已经遍历过所以不计入）中寻找权值最小的边。（上图为顶点1）将其添加至A类中。大家注意在这里我们去掉了权值为18的边，这是因为从顶点1可以通过权值为14的边到达顶点6，从顶点3可以通过权值为18的边到达顶点6，根据定义我们要寻找顶点间权值最小的边，所以我们用权值为14的边替换权值为18的边。

  

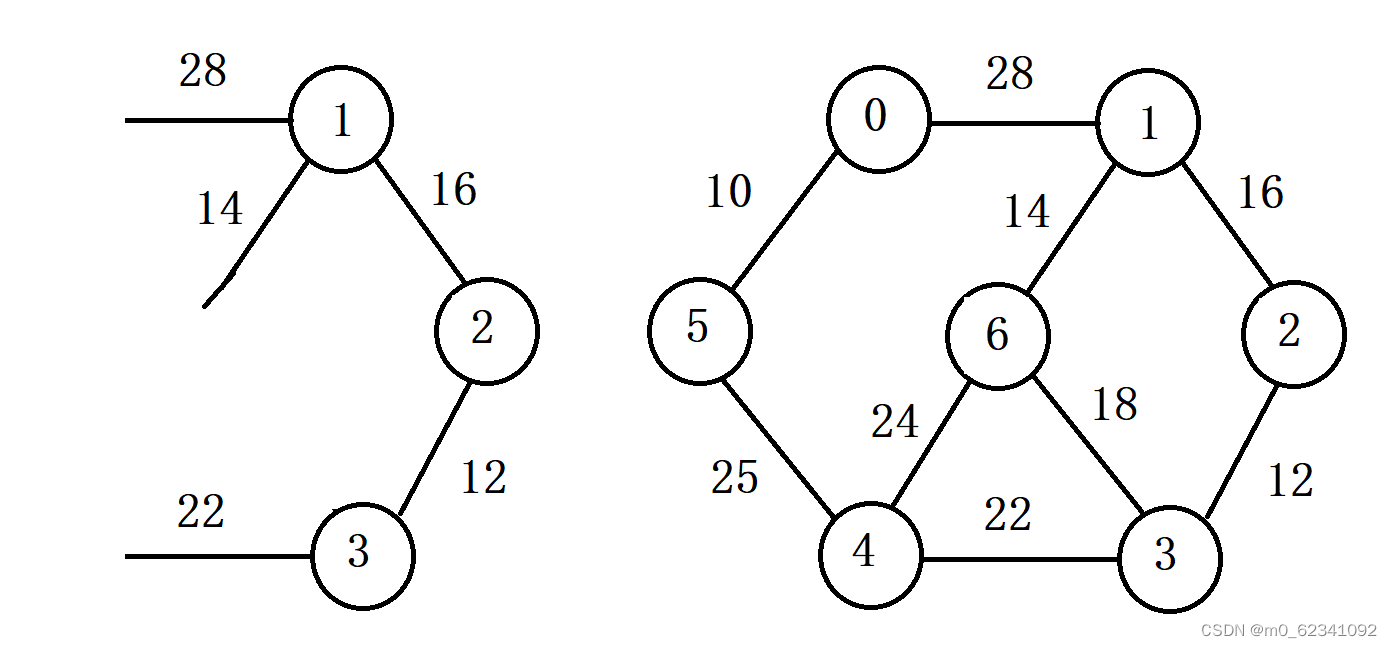
  步骤同上。在现有的三条边中寻找权值最小的边。（上图为顶点6）将其添加至A类。大家注意在这里增加顶点6，之后我们本应该可以获得一条从顶点6到顶点4权值为24的边，但是由于我们有从顶点3到顶点4的权值为22的边，所以根据定义，我们无需添加顶点6到顶点4权值为24的边

  

  重复上述步骤。我们就可以通过prim算法得到最终的最小生成树。

  

  看完了讲解，接下来让我们看看prim算法的代码实现吧！

  三、代码实现

  \*
  #define MAXV 
  #define INF 32767      //定义无穷大
  typedef struct {
  	int no;            //顶点的编号
  	InfoType info;    //顶点的其他信息
  }VertexType;           //顶点的类型
  typedef struct {
  	int edges[MAXV][MAXV];   //邻接矩阵数组
  	int n, e;                //顶点数，边数
  	VertexType vexs[MAXV];   //存放顶点信息
  }MGraph;                   //完整的图邻接矩阵类型
  *\
  void Prim(MGraph g,int v) {  //传入一个邻接矩阵，和起始顶点
      int lowcost[MAXV];
      int closest[MAXV];
      int min;
  	int i,j,k = 0;
      for (i=0; i          //给lowcost[]和closest[]置初值
          lowcost[i]=g.edges[v][i];
          closest[i]=v;
      }
      lowcost[v] = 0;
      for (i=1; i           //找出n-1个顶点
          min=INF;
          for (j=0; j     //在(V-U)中找出离U最近的顶点k
              if (lowcost[j]!=0 && lowcost[j]