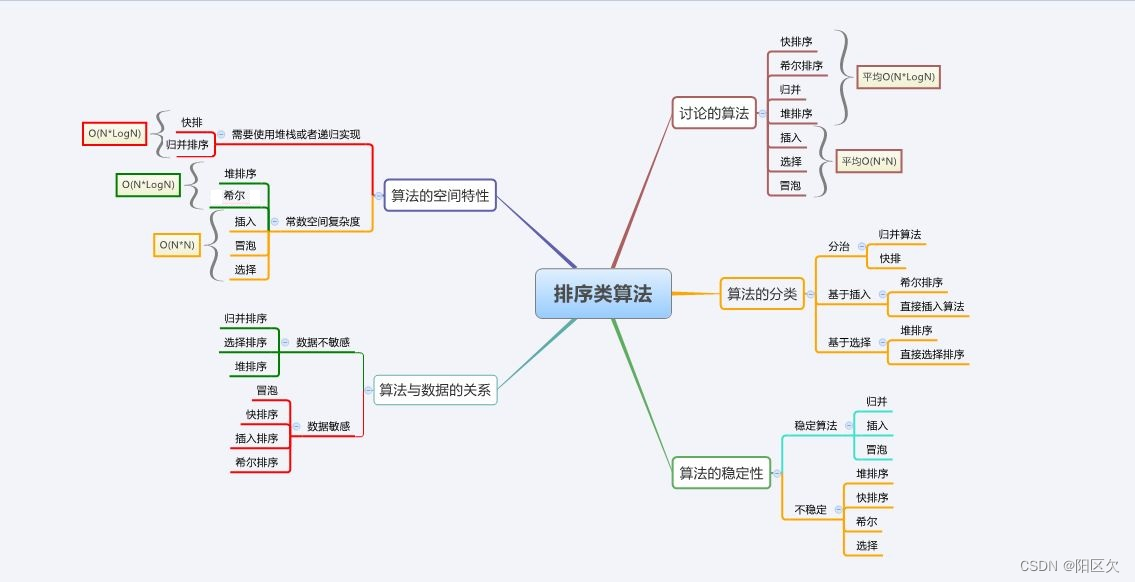
【数据结构】排序算法
目录
常见的排序算法：
插入排序：
选择排序：
交换排序：
归并排序：
排序算法复杂度及稳定性分析：
编辑 排序介绍与实现：
1.直接插入排序
2.希尔排序
3.选择排序
4.堆排序
5.冒泡排序
6.快速排序hoare版本
7.快速排序挖坑版本
8.快速排序指针版本
9.快速排序非递归版本
10.归并排序
11.归并排序非递归版本
本篇文章主要是介绍一些数据结构的基础排序算法。
常见的排序算法：
插入排序：
- 直接插入排序
- 希尔排序
选择排序：
- 选择排序
- 堆排序
交换排序：
- 冒泡排序
- 快速排序
归并排序：
- 归并排序
排序算法复杂度及稳定性分析：
排序介绍与实现：
1.直接插入排序
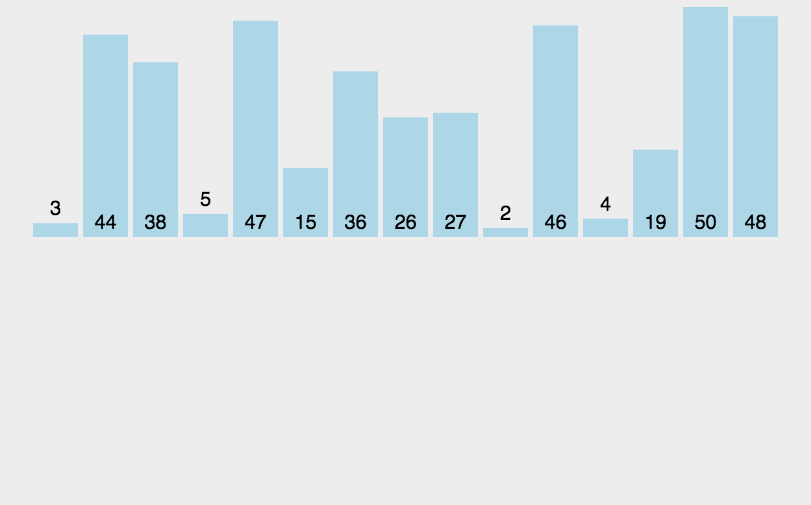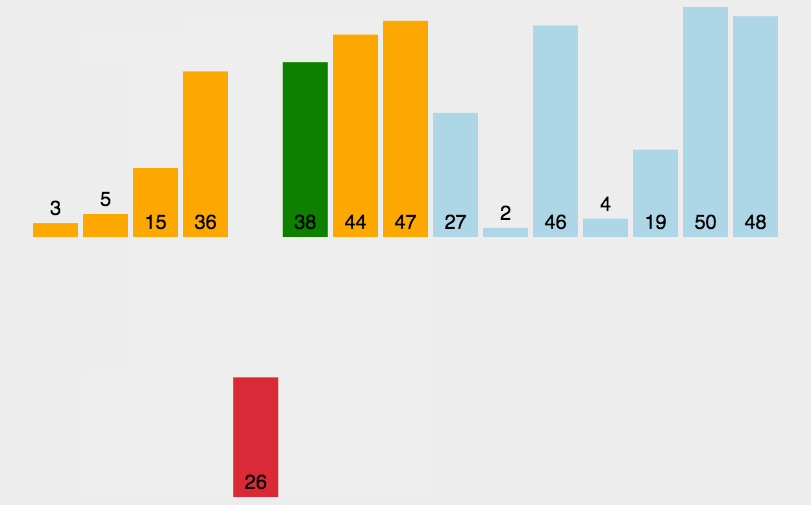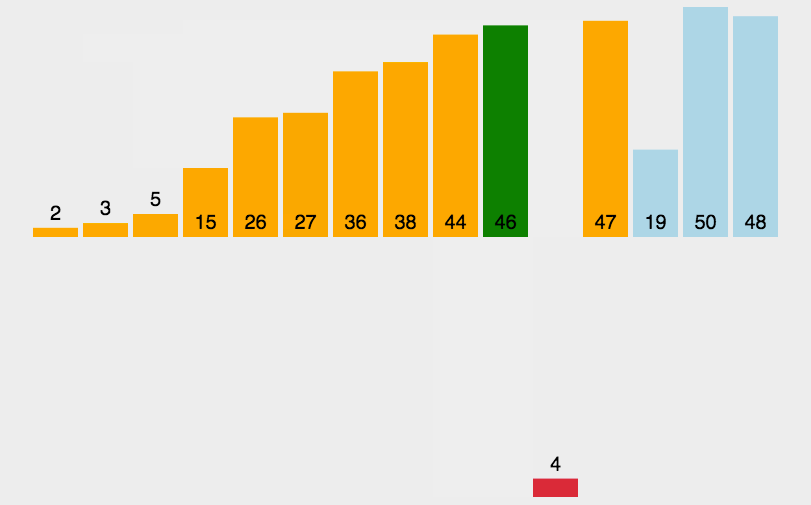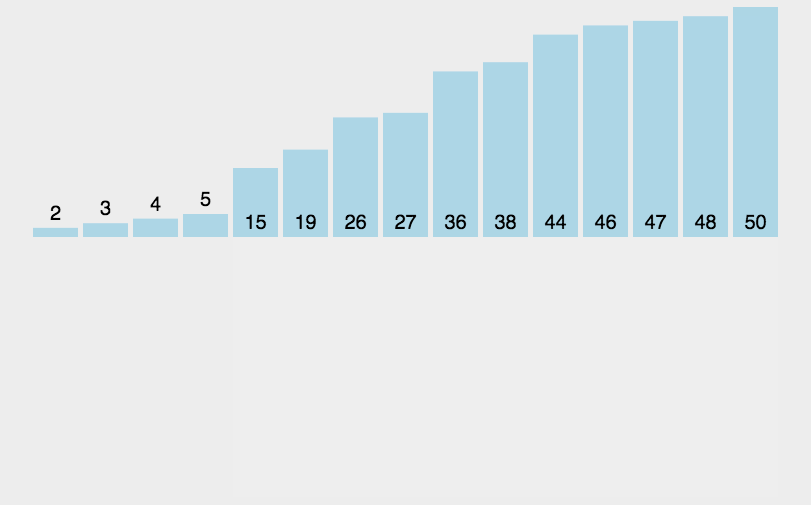
动图演示：
直接插入排序是认为要插入数之前的所有数据已经排序好，用一个tmp临时变量存储要插入的值，如果要插入值的前一个数据比他大，那么就向后覆盖，接着继续往前比，直到遇到比要插入值小的数据，将要插入值插入在该数据的后一位。
代码演示：
void Insert_Sort(int* a, int n)
{
// 这边由于要取值到end+1，所以end的最大值为n-2,所以 i = 0) // end为下标，最坏的比较情况是插入值小于a[0]
{
if (a[end] > tmp)
{
a[end + 1] = a[end];// 如果插入数小则向后覆盖
--end; // 继续比较前一个，如果比较的是a[0]，那么当前的end= 0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
--end;
}
else {
a[end + 1] = tmp;
break;
}
}
// 特殊情况如果插入值比a[0]还小，end1)
{
gap = gap / 3 + 1; // 算取初始gap
// 写法一：
// 以组排序
// 先排序第一组，也就是用相同颜色线连接的数据
for (int i = 0; i = 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else {
break;
}
}
a[end + gap] = tmp;
}
}
// 写法二：
// 一个一个排序
// 从0~n-gap数据
for (int i = 0; i = 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else {
break;
}
}
a[end + gap] = tmp;
}
}
}
3.选择排序
静态图介绍：
选择排序是从数据的首端去进行选择，遍历一遍数组取选出最大值和最小值，选出后交换放在两端排序，继续去选择。注意的是如果最大值是第一个数据，后面交换时会出现数据被替代的情况，这种情况下我们需要在交换后将最大值下标指向最小值下标。
代码演示：
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void Select_Sort(int* a, int n)
{
int begin = 0;
int end = n - 1;
while (begin
4.堆排序
静态图介绍：
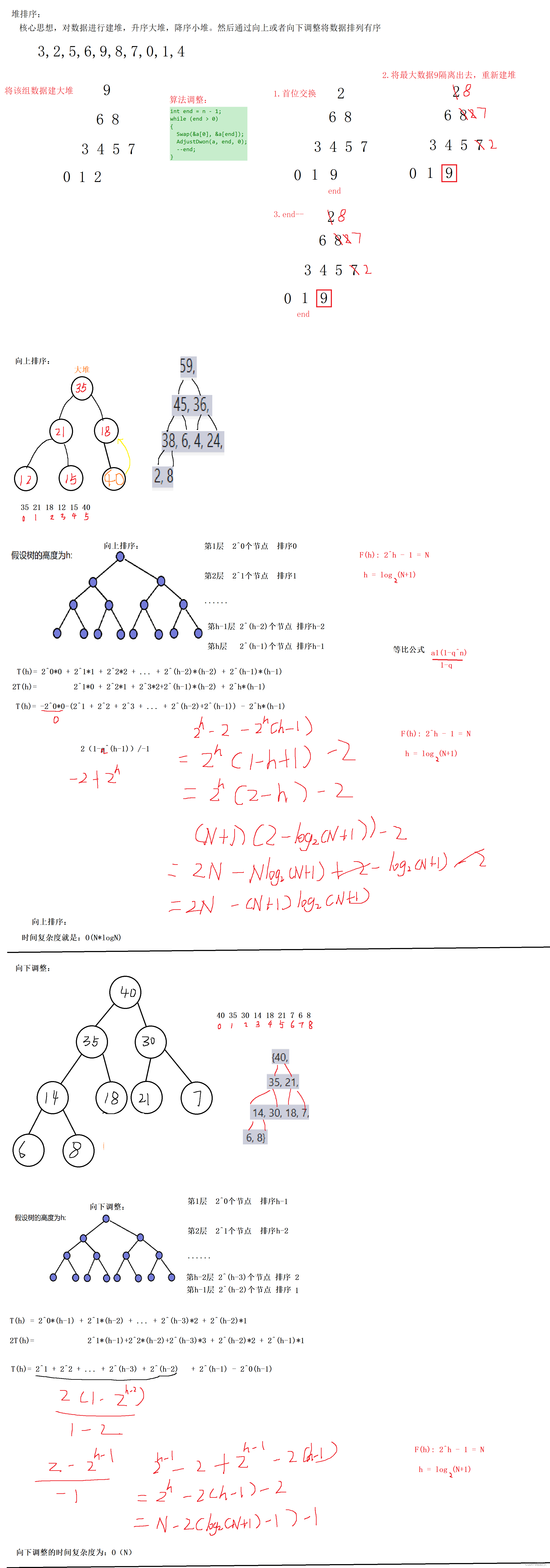
堆排序之前需要对数据进行建堆处理，建堆分为大堆，小堆，大堆指的是所有父亲节点的值都要大于孩子节点；小堆指的是所有父亲节点的值都要小于孩子节点。建堆又可以分为向上调整和向下调整，向上调整指的是将数据插入末尾，然后根据什么堆型去进行调整；向下调整指的是第一个父亲节点位置开始根据堆型情况向下进行调整。 建完堆最后的排序需要使用向下调整，升序建大堆，降序建小堆。
代码演示：
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void AdjustUp(int* a, int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
parent = (child - 1) / 2;
}
else {
break;
}
}
}
void AdjustDown(int* a, int n, int parent)
{
int child = parent * 2 + 1;
while (child a[child] && child + 1 a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else {
break;
}
}
}
void Heap_Sort(int* a, int n)
{
// 建堆
// i 起始为第一个父亲节点
// 方法1：使用向下调整建堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
// 方法2：使用向上调整建堆
for (int i = 0; i 0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
--end;
}
}
5.冒泡排序
动图演示：
冒泡排序是前一项和后一项进行比较，如果大就进行交换，然后将数据一直冒到最后放置。冒泡排序可以进行一次优化，使用flag进行记录，如果遍历一次没有进行交换说明是有序的，直接跳出循环。
代码演示：
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void Bubble_Sort(int* a, int n)
{
for (int i = 0; i
6.快速排序hoare版本
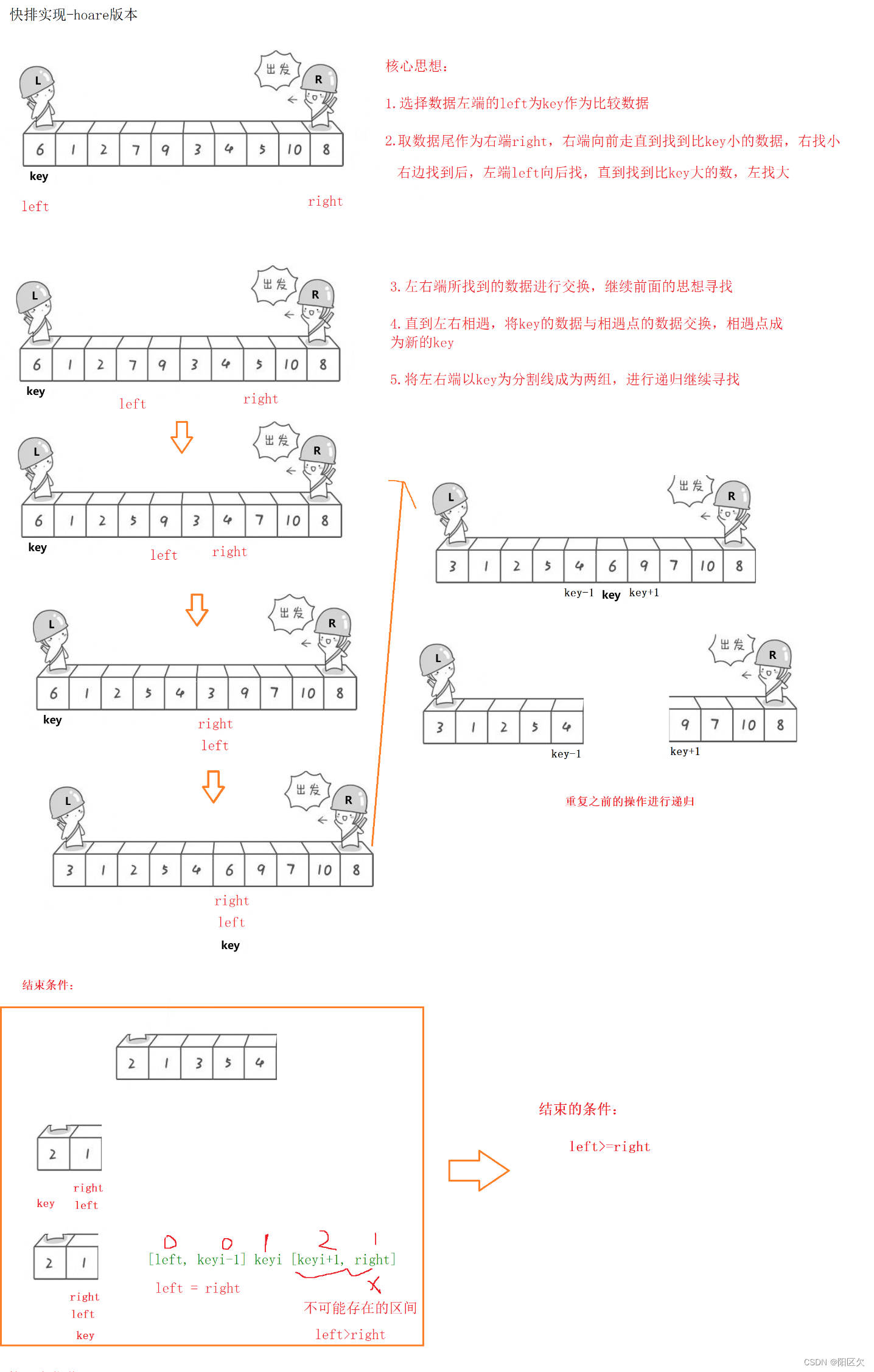
hoare版本动态演示图：
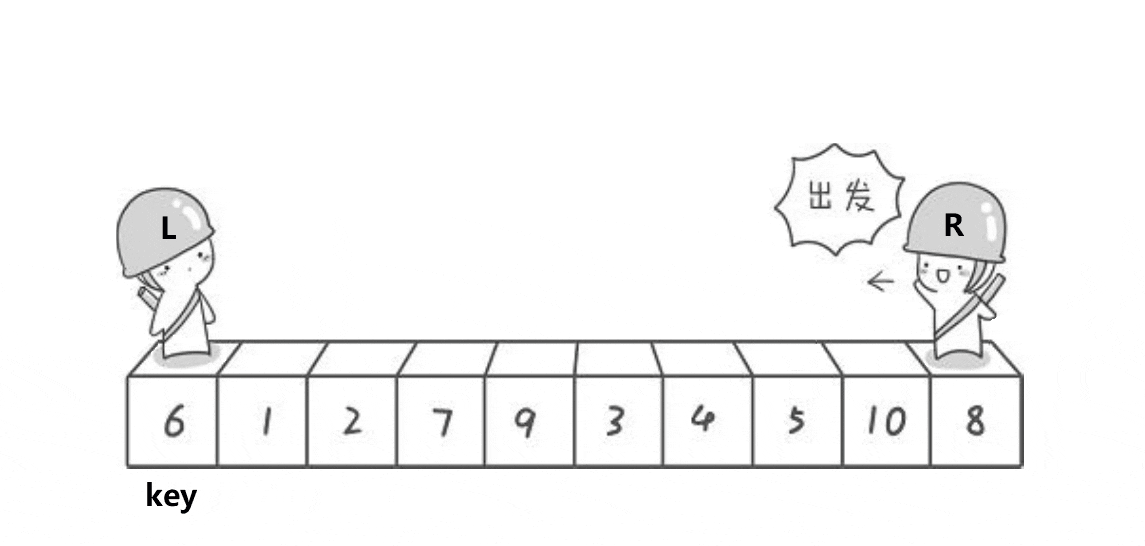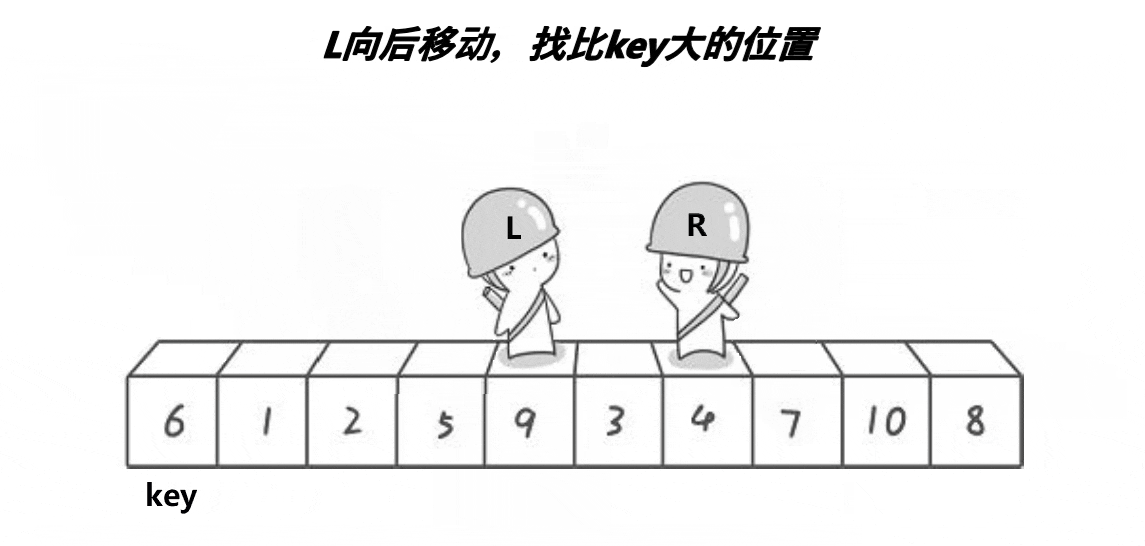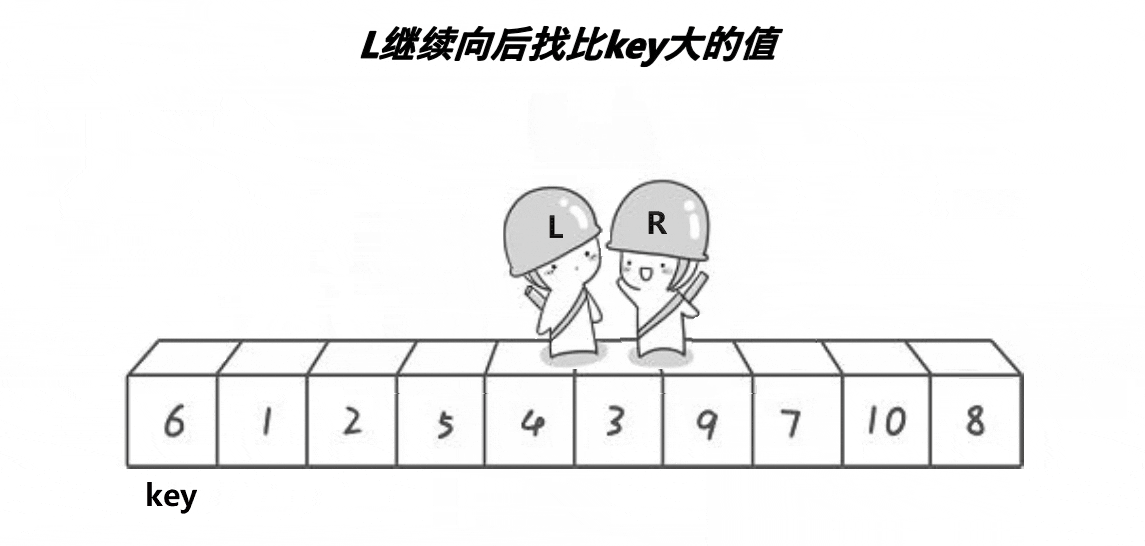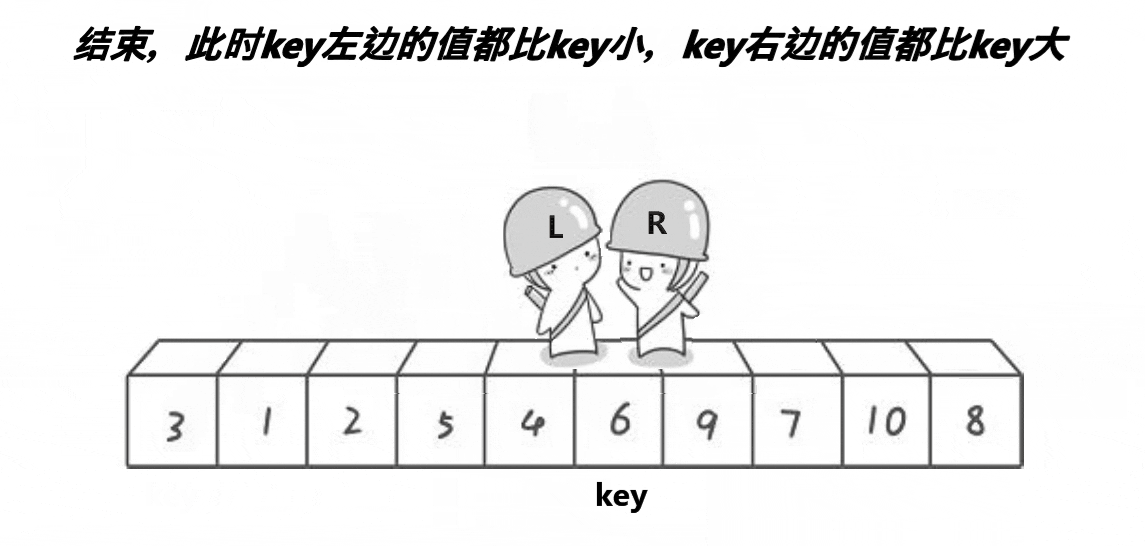该版本的快速排序通过定义数据左端的首数据为key，然后分别从左右两端开始找，先从右端找比key小的数据，再从左端找比key小的数据，交换。最后左右相遇的位置与key指向的数据交换，并且成为新的key。
新的可以划分成两个区域，递归继续往下调整。
代码实现：
void Quick_Sort_hoare(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int keyi = left;
int begin = left, end = right;
while (begin = a[keyi] && begin a[right]) // right a[left]) // mid
小区间优化：
这边推荐使用插入排序，优点是实现容易，并且对于快有序的数据的排序效率也高。
void Insert_Sort(int* a, int n)
{
// 这边由于要取值到end+1，所以end的最大值为n-2,所以 i = 0) // end为下标，最坏的比较情况是插入值小于a[0]
{
if (a[end] > tmp)
{
a[end + 1] = a[end];// 如果插入数小则向后覆盖
--end; // 继续比较前一个，如果比较的是a[0]，那么当前的end= 0)
{
if (a[end] > tmp)
{
a[end + 1] = a[end];
--end;
}
else {
a[end + 1] = tmp;
break;
}
}
// 特殊情况如果插入值比a[0]还小，end a[right]) // right a[right]) // right a[left]) // mid = right)
{
return;
}
if ((right - left + 1) = a[keyi] && begin
当然该版本也可以加入之前版本的优化。
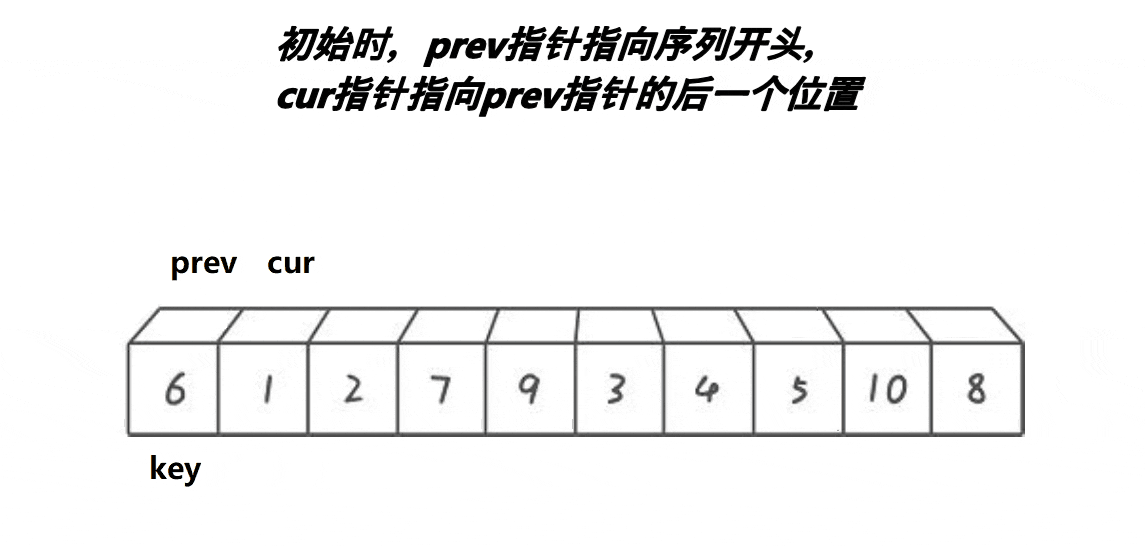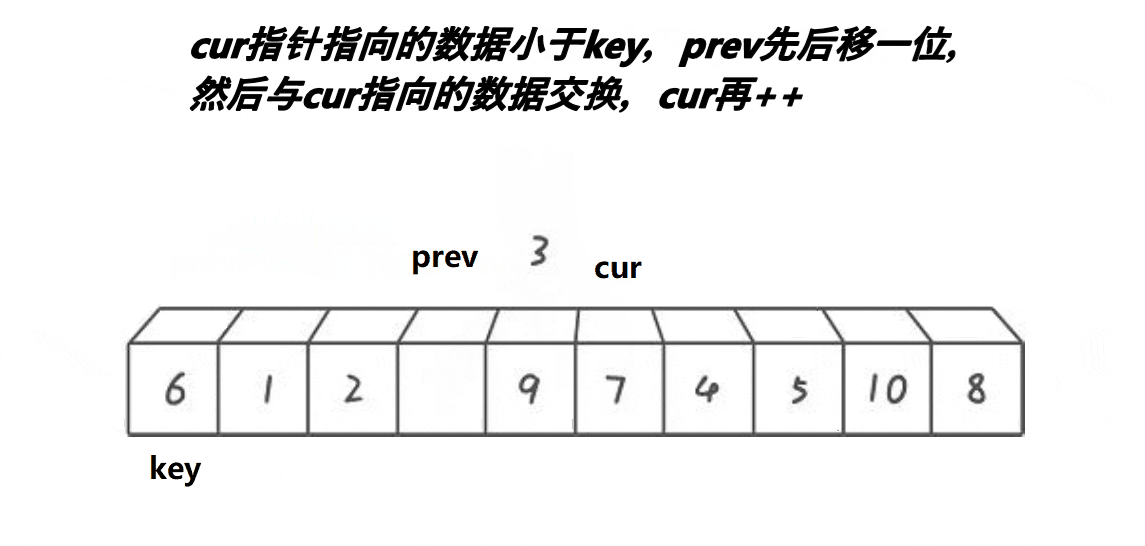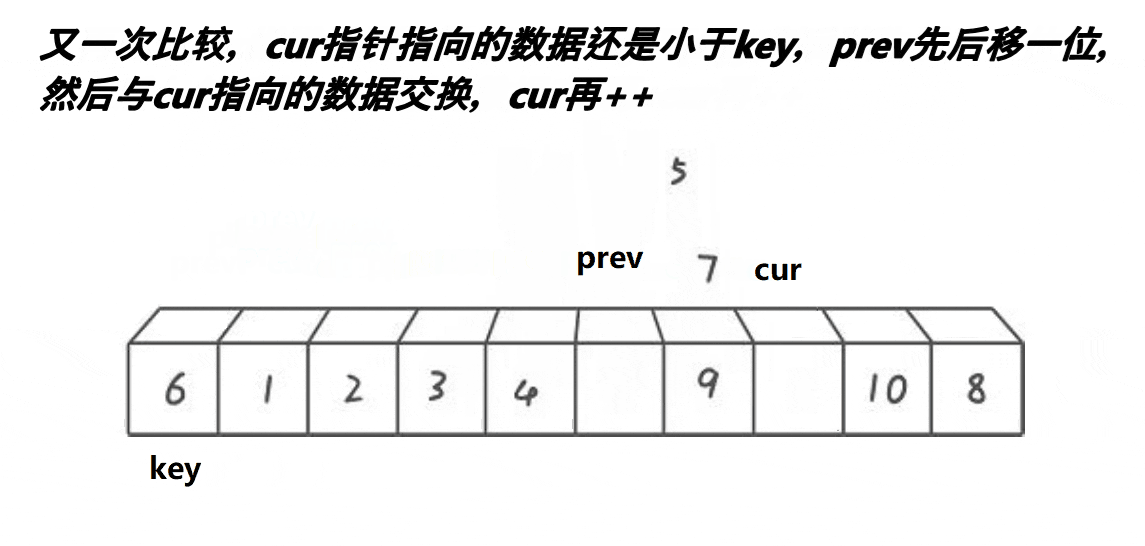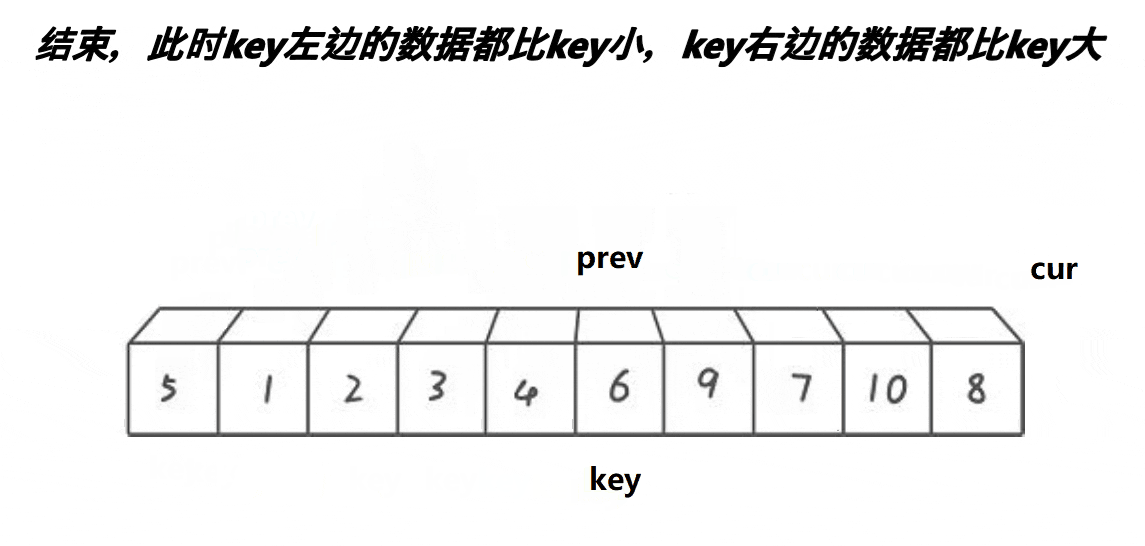
8.快速排序指针版本
动态演示图：
用key记录比较数据下标，然后创建prev和cur指针，prev指针从首位置开始，cur指针指向prev的下一个位置，cur指针向前走，如果cur指向的数据小于key下标指向的数据，那么prev++，prev和cur指向的数据交换，cur++；如果cur指向的数据大于key下标指向的数据，cur指针继续向前走，直到cur指针超过right范围，prev指向的数据和key的数据交换，prev的位置成为新的key。
代码实现：
void Quick_Sort_Point(int* a, int left, int right)
{
if (left >= right)
{
return;
}
int keyi = left;
int prev = left;
int cur = prev + 1;
while (cur 
