第三章 搜索与图论（二）（最短路）

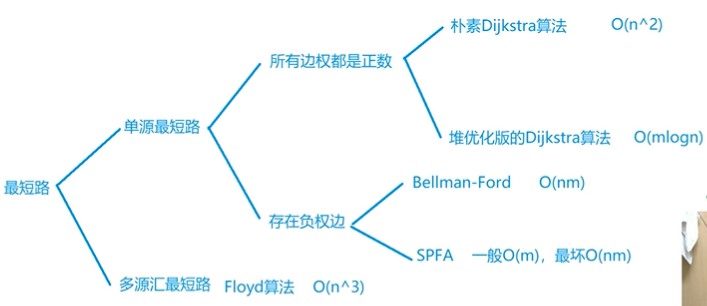
一、最短路问题

1、对于稠密图，由于朴素版的dijkstra算法与边数无关使用这种算法的复杂度较低。稀疏图用堆优化版的算法；单源最短路中存在负权边用SPFA 算法通常较好；多源用floyd算法；

 难点：如何建图，抽象为最短路问题。

二、朴素版dijkstra算法

由于稠密图用这种算法，邻接矩阵存图，注意把g初始化为0x3f；st保存每个数组的状态，

#include
//849dijkstra最短路
using namespace std;
const int N=510;
int g[N][N],disk[N],st[N];
int n,m;
int dijkstra()
{
   disk[1]=0;
   for(int i=1;in>>m;
    memset(disk,0x3f,sizeof disk);//初始化最短路为正无穷
    memset(g,0x3f,sizeof g);
    memset(st,-1,sizeof st);
    for(int i=0;i>a>>b>>c;
        //由于存在重复带权边，所以要留住那个较短的边因此初始化g为无穷
        g[a][b]=min(g[a][b],c);
    }
    int t=dijkstra();
    cout>m;
    memset(disk,0x3f,sizeof disk);//初始化最短路为正无穷
    memset(st,-1,sizeof st);
    memset(h,-1,sizeof h);
    for(int i=0;i>a>>b>>c;
        add(a,b,c);
    }
    int t=dijkstra();
    cout>k;
    for(int i=0;i>a>>b>>w;
       edges[i]={a,b,w};//保存边
    }
    int t=bellman_ford();
    if(t==-1)puts("impossible");
    else cout>m;
  memset(h,-1,sizeof h);
  while(m--)
  {
      int a,b,c;
      cin>>a>>b>>c;
      add(a,b,c);
  }
  int t=spfa();
  if(t==-1)puts("impossible");
  else cout>m;
  memset(h,-1,sizeof h);
  while(m--)
  {
      int a,b,c;
      cin>>a>>b>>c;
      add(a,b,c);
  }
  int t=spfa();
  if(spfa())puts("Yes");
  else puts("No");
}

六、弗洛伊德Floyd算法求多源最短路

三重循环

#include
//852 spfa判断是否
using namespace std;
const int N=210,INF=1e9;
int d[N][N];
int n,m,Q;
void floyd()
{
    for(int k=1;k>m>>Q;
    for(int i=1;ia>>b>>c;
       d[a][b]=min(d[a][b],c);
    }
    floyd();
    while(Q--)
    {
        int a,b;
        cin>>a>>b;
        if(d[a][b]