Matlab: ode45解微分方程——以弹簧振子模型为例

简介：

在科学和工程中，我们经常遇到描述事物变化的微分方程。这些方程可以帮助我们理解从行星运动到药物在体内的扩散等各种现象。但是，很多微分方程非常复杂，手动求解几乎不可能。这时，我们就可以使用像 ode45这样的工具来帮助我们找到解决方案。下面谈谈ode45函数的基本用法以及简单应用。

一、ode45()概念与用法

ode45 是 MATLAB 中用于求解常微分方程初值问题的函数，它采用了一种称为 “Runge-Kutta 方法” 的数值积分技术。具体来说，ode45 使用了一种称为 “Dormand-Prince” 方法的五阶龙格-库塔公式，同时还使用了一个自适应步长控制算法，以保证数值解的精度和稳定性。

ode45 的基本用法如下：

[t, y] = ode45(@odefun, tspan, y0)

• @odefun 是一个函数句柄，表示待求解的微分方程组。这个函数接受两个参数：时间 t 和状态向量 y，并返回对应的导数值。
• tspan 是一个包含两个元素的数组，表示求解的时间区间 [t_start, t_end]。
• y0 是一个包含微分方程组初始状态的列向量。

  ode45 返回两个输出参数：

  • t 是一个列向量，包含求解过程中的时间点。
  • y 是一个大小为 (length(t), length(y0)) 的矩阵，每一行表示对应时间点 t 处的状态向量 y。

    二、ode45()步骤流程方法

    使用 ode45 解微分方程组的步骤通常包括：

    1. 定义方程：首先，需要将问题转化为一个或多个微分方程。

    2. 编写函数：在 MATLAB 中，你需要编写一个函数来定义这些方程。这个函数将接受当前的状态（比如位置和速度）和时间作为输入，并返回状态的导数（比如加速度）。

    3. 调用 ode45：使用 `ode45` 函数，输入你的方程函数、初始条件、时间跨度等参数。

    4. 分析结果：ode45 将返回一个近似的数值解，你可以用它来进行进一步的分析或绘图。

    三、弹簧振子模型代码实践

    有一个挂在天花板上的弹簧，下面挂着一个质量为 m 的物体。如果把这个物体拉下来一点然后放手，它会开始上下振动，这就是一个弹簧振子系统。这个系统的运动可以通过一个二阶微分方程来描述：

     

    为了使用 ode45，我们需要将这个二阶方程转换为一阶方程组。我们引入一个新的变量 v = dx/dt，表示物体的速度。那么加速度 d^2x/dt^2 就可以表示为 dv/dt。这个过程有点像状态空间方程的改写。现在我们有两个方程： 

    

    

     现在，我们可以按照以下步骤使用 ode45：

    1.定义方程，编写函数：

    function dxdt = spring_system(t, x)
        m = 1;  % 质量 m
        k = 4;  % 弹簧常数 k
        dxdt = [x(2); -k/m * x(1)];  % 返回速度和加速度
    end

     2.调用ode45:

    % 从 t=0 到 t=10，初始位置为 1，初始速度为 0
    [t, x] = ode45(@spring_system, [0, 10], [1, 0]); 

    3.分析结果：

    plot(t, x(:,1), 'r', 'LineWidth', 2); % 绘制位置随时间变化的图
    hold on;
    plot(t, x(:,2), 'b', 'LineWidth', 2); % 绘制速度随时间变化的图
    xlabel('Time');
    ylabel('Displacement/Velocity');
    legend('Displacement', 'Velocity');

    四、完整代码 

    下面给出完整代码：

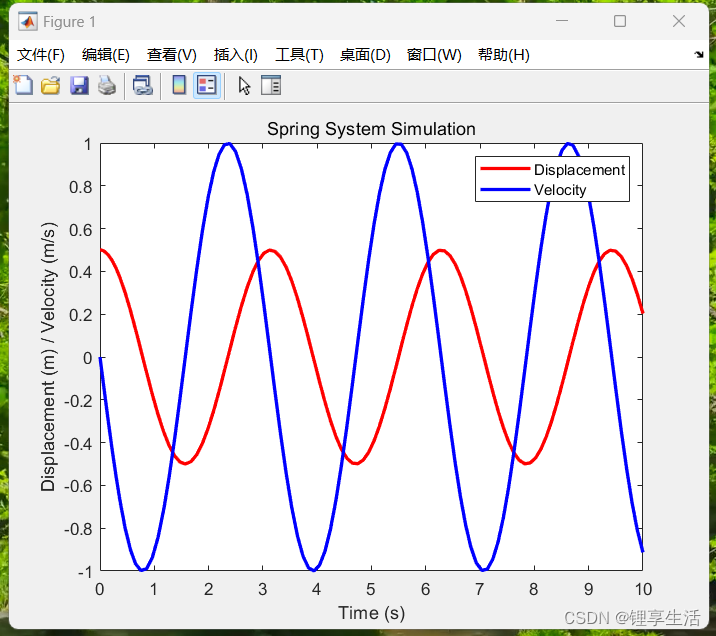
    % 模拟参数
    tspan = [0 10];  % 时间区间
    x0 = [0.5; 0];  % 初始条件，假设初始位置为 0.5 m，初始速度为 0 m/s
    % 使用 ODE45 求解微分方程
    [t, x] = ode45(@spring_system, tspan, x0);  %x中接收到的是函数返回值的原函数位移和速度
    % 绘图
    figure;
    plot(t, x(:,1), 'r', 'LineWidth', 2); % 绘制x随时间变化的图（位置）
    hold on;
    plot(t, x(:,2), 'b', 'LineWidth', 2); % 绘制x的导数随时间变化的图（速度）
    xlabel('Time (s)');
    ylabel('Displacement (m) / Velocity (m/s)');
    legend('Displacement', 'Velocity');
    title('Spring System Simulation');
    % 局部函数定义：定义微分方程系统
    function dxdt = spring_system(t, x)
        m = 1;  % 质量 m
        k = 4;  % 弹簧常数 k
        dxdt = [x(2); -k/m * x(1)];  % 返回速度和加速度
    end