C语言王国——杨氏矩阵

目录

1. 引言

 2. 了解杨氏矩阵

3. 思路分析

4. 代码

 5. 总结

---

1. 引言

最近在做二维数组的训练的时候发现了一个很有意思的题：

一看这不是杨氏矩阵嘛，接下来就由姜糖我带大家了解一下这个著名的矩阵。

 2. 了解杨氏矩阵

通过查阅百度得知：

杨氏矩阵：

是对组合表示理论和舒伯特演算很有用的工具。它提供了一种方便的方式来描述对称和一般线性群的群表示，并研究它们的性质。有一个二维数组. 数组的每行从左到右是递增的，每列从上到下是递增的. 在这样的数组中查找一个数字是否存在。 时间复杂度小于O(N)。

平常我们在数组里查找数字时，是否我们用的都是暴力遍历查找，一个数一个数的去比对时间复杂度为O(n)，效率很低，这时候就该我们杨氏矩阵出场了。 

---

3. 思路分析

资料中我们知道了杨氏矩阵是一个二维数组，数组的每行从左到右是递增的，每列从上到下是递增的. 在这样的数组中查找一个数字是否存在，所以我们举一个例子：

在arr[3][3] = {{1,2,3},{4,5,6},{7,8,9}}查找数字n。

数组如图：

此数组符合杨氏矩阵。

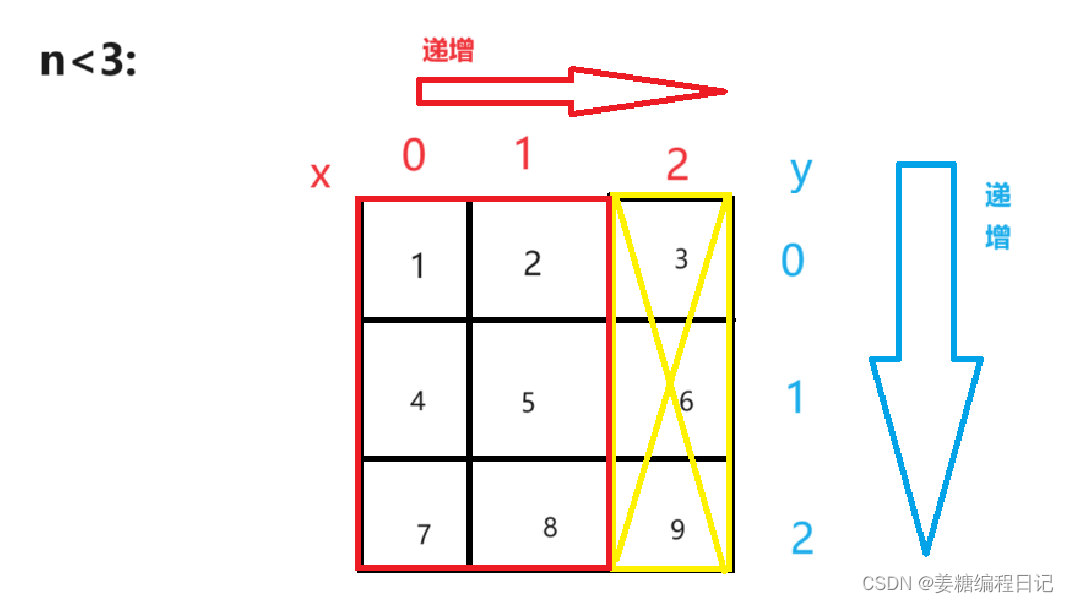
那接下来我们该怎么查找数字更快捷呢。接下来我们要找此数组里的特殊的数，我们会发现最右上角的那个数是一行之中最大的一列之中最小的所以我们拿n去跟他比较，然后我们就会发现：

红色为查找范围，黄色为除去范围。

根据图中我们发现当n>3时，第一行就被排除了，查找范围只有第二、三行；

当n= 0; j--) { if (n == arr[i][j]) { return 1; } else if(n > arr[i][j]) { break; } } } return 0; } int main() { int arr[3][3] = { 1,2,3,4,5,6,7,8,9 }; printf("输入你要查找的数字："); int n = 0; scanf("%d", &n); int ret = young(arr, n); if (n) { printf("找到了"); } else printf("找不到"); return 0;

但是我们发现这样子的代码只能判断是否找到数字，不能判断数字的位置，所以我给代码进行了优化：

#include
int young(int(*arr)[3], int* px, int* py, int n)
{
	int y = *py;
	int x = *px-1;
	for (*py = 0; *py = 0; (*px)--)
		{
			if (n == arr[(*py)][(*px)])
			{
				return 1;
			}
			else if (n > arr[*py][*px])
			{
				break;
			}
		}
	}
	return 0;
}
int main()
{
	int arr[3][3] = { 1,2,3,4,5,6,7,8,9 };
	printf("输入你要查找的数字：");
	int n = 0;
	scanf("%d", &n);
	int i = 3;
	int j = 3;
	int ret = young(arr, &i , &j , n);
	if (n)
	{
		printf("找到了为arr[%d][%d]",j,i);
	}
	else
		printf("找不到");
	return 0;
}

像这样子我们把数组行和列用指针的形式传到函数里去，随着函数的变化去变化最后就能得到数组中我们要查找的n的位置。 

最后我们发现用while循环思路会更清晰准确：

#include
int find_num(int arr[3][3], int* px, int* py, int k)
{
	int x = 0;
	int y = *py - 1;
	while (x = 0)
	{
		//向下查找
		if (k > arr[x][y])
		{
			x++;
		}
		//向左查找
		else if (k  
 5. 总结
 
如果大家有不同见解也可以私信姜糖哦，姜糖也在不停的学习进步，与大家一起步入大牛之列。期待大家三连！！