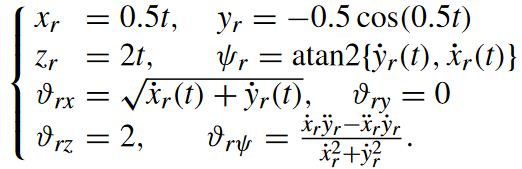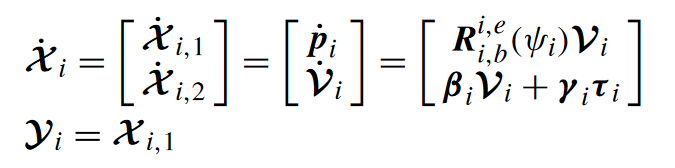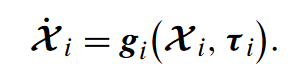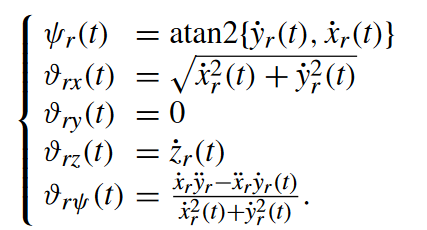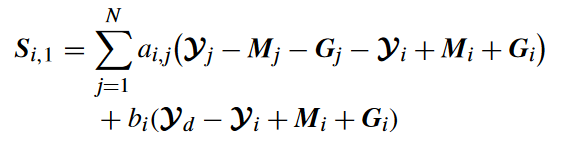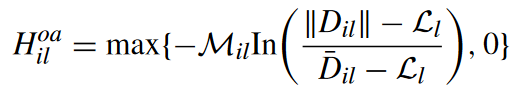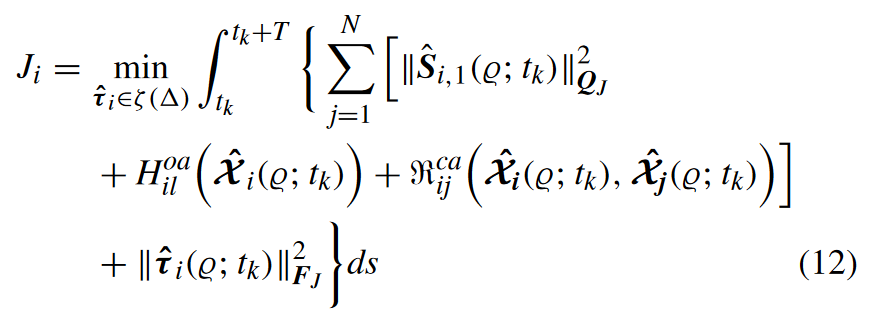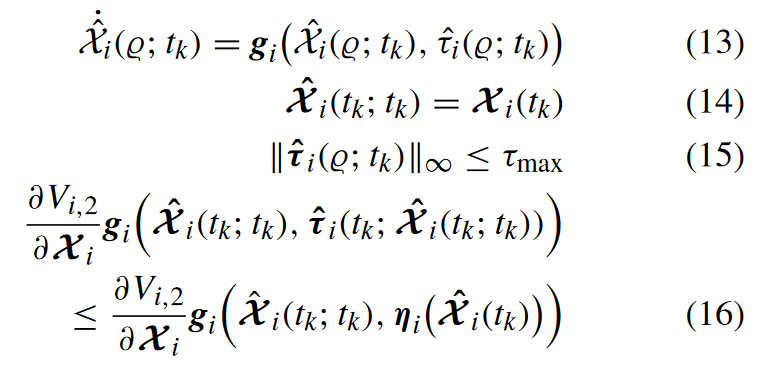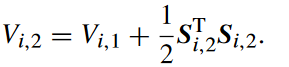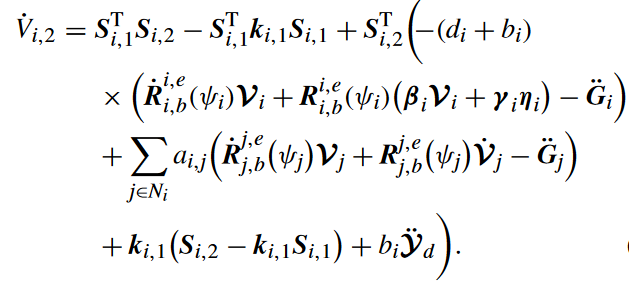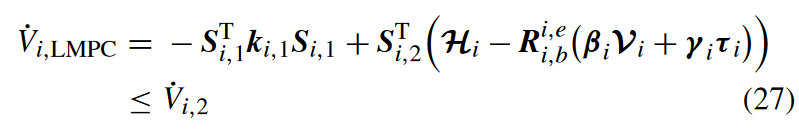【paper】多无人机避障 - 模型预测编队跟踪控制
- Model Predictive Formation Tracking-Containment Control for Multi-UAVs With Obstacle Avoidance
- 2024.1
- IEEE TRANS ON SYSTEMS, MAN, AND CYBERNETICS: SYSTEMS【Q1 8.7】
- Zhixu Du 同济大学
Q1 Background:本文试图解决一个什么样的问题?
- 三维环境中多机避障 + 编队跟踪包围(Formation Tracking-Containment)控制问题。
- 在初始阶段,无人机群需要跟踪(tracking)特定的目标。一旦达到预设时间,无人机群就会从跟踪控制切换到包围(containment)控制,将目标围到凸包上。
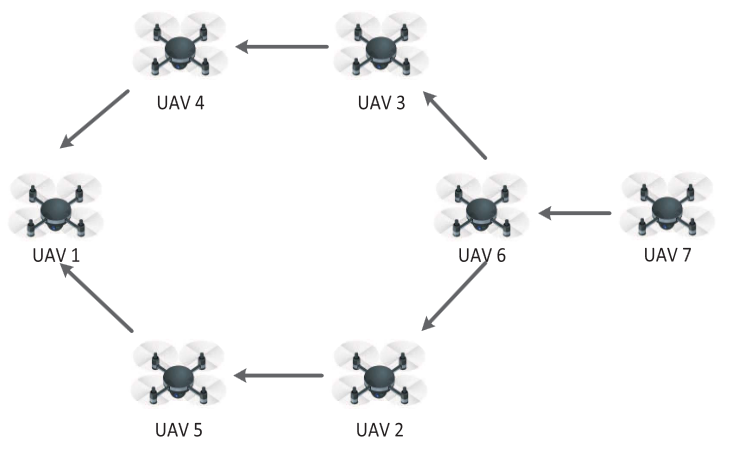
👉7台无人机,第7台为被跟踪目标
👉其他6台无人机编队相对距离
👉编队切换时间15S
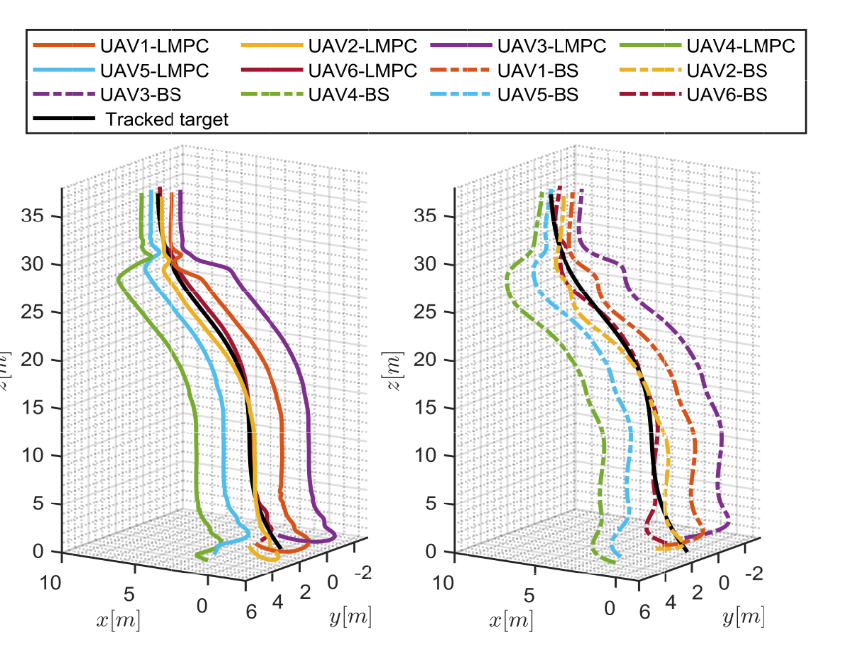
- 无障碍物场景
👉3D轨迹图。实线是本文LMPC方法,虚线是反推方法
👉X Y 轴编队误差
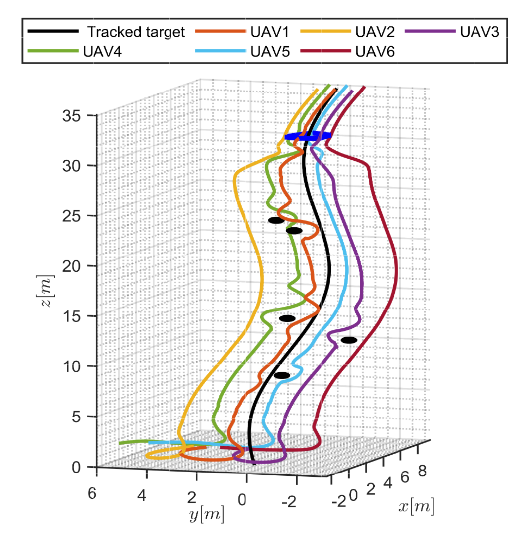
- 有障碍物场景
Q2 What’s Known:之前解决这个问题有哪些方法?
- 编队控制:滑膜 \ PID \ MPC \ backstepping control
- MPC:
- 传统的MPC策略使用无限的预测时域或在成本函数中添加终端惩罚项来实现闭环系统稳定性,隐式的,比较困难;
- 使用李雅普诺夫LMPC保证稳定性:以前的工作仅适用于Tracking任务,agent遵循固定距离的轨迹曲线,不适用于Tracking-Containment
- 跟踪包围:交换交互拓扑 \ 虚拟管(北航全权,这篇之后看一下)\ 基于邻居的拓扑结果 \ 切换函数
- 存在缺陷:瞬态切换可能导致通信拓扑结构的崩溃 \ 不够平滑(因为需要反应式避碰和预测性调整位置来稳定跟踪包围动态目标)
- 避障:基于APF的LMPC
- 存在缺陷:仅考虑单个障碍物、集中式的拓扑通信,缺少用LMPC框架解决无人机在具有多个障碍物场景的跟踪包围问题。
北航全权:Multi-UAV cooperative target encirclement within an annular virtual tube
Q3 What’s New:本文是用什么样的方法如何解决这个问题的?
- LMPC;构造一个平稳的过渡函数, 将避障函数引入成本项,基于反推设计(backstepping)设计了辅助控制器
η
i
\eta_{i}
ηi 作为约束保证闭环稳定性
建模
拓扑
-
N + 1 N+1 N+1台智能体, N N N台跟踪1台,被跟踪的这台无人机标号为N+1号
-
有向图, G = ( N , E , A ) \mathcal{G}=(\mathcal{N},\mathcal{E},A) G=(N,E,A), a i j > 0 a_{ij} > 0 aij>0表示 j j j传信息给 i i i;拉普拉斯矩阵 Υ ˉ = L − A \bar{\boldsymbol{\Upsilon}}=\boldsymbol{L}-\boldsymbol{A} Υˉ=L−A, L \boldsymbol{L} L是入度矩阵
-
增广图, G ˉ = ( N ˉ , E ˉ ) \bar{\mathcal{G}}=(\bar{\mathcal{N}},\bar{\mathcal{E}}) Gˉ=(Nˉ,Eˉ); B ˉ = diag { b 1 , … , b N } ∈ R N × N \bar{\boldsymbol{B}}=\operatorname{diag}\{b_1,\ldots,b_N\}\in\mathbb{R}^{N\times N} Bˉ=diag{b1,…,bN}∈RN×N, b > 0 b>0 b>0表示能够从N+1号无人机获得信息
-
被跟踪无人机具有指向所有其他跟踪无人机的路径(有一颗有向生成树)假设1
-
Υ
ˉ
+
B
ˉ
\bar{\boldsymbol{\Upsilon}}+\bar{\boldsymbol{B}}
Υˉ+Bˉ是非奇异的
四旋翼模型
- 👉
p
i
=
[
x
i
,
y
i
,
z
i
,
ψ
i
]
T
∈
R
4
p_i=[x_i,y_i,z_i,\psi_i]^\mathrm{T}\in\mathbb{R}^4
pi=[xi,yi,zi,ψi]T∈R4是xyz三维位置+偏航角,
👉 V i = [ ϑ i x , ϑ i y , ϑ i z , ϑ i ψ ] T ∈ R 4 \mathcal{V}_i=[\vartheta_{ix},\vartheta_{iy},\vartheta_{iz},\vartheta_{i\psi}]^\mathrm{T}\in\mathbb{R}^4 Vi=[ϑix,ϑiy,ϑiz,ϑiψ]T∈R4是相应的线速度+航向角速度。
👉 τ i = [ τ i x , τ i y , τ i z , τ i ψ ] T ∈ R 4 \tau_{i}=[\tau_{ix},\tau_{iy},\tau_{iz},\tau_{i\psi}]^{\mathrm{T}}\in\mathbb{R}^{4} τi=[τix,τiy,τiz,τiψ]T∈R4是控制输入(速度)
- 👉
β
i
=
d
i
a
g
(
−
[
1
/
L
i
x
]
,
−
[
1
/
L
i
y
]
,
−
[
1
/
L
i
z
]
,
−
[
1
/
L
i
ψ
]
)
∈
R
4
×
4
\boldsymbol{\beta_i} = diag( - [ 1/ L_{ix}] , - [ 1/ L_{iy}] , - [ 1/ L_{iz}] , - [ 1/ L_{i\psi }] ) \in\mathbb{R} ^{4\times 4}
βi=diag(−[1/Lix],−[1/Liy],−[1/Liz],−[1/Liψ])∈R4×4;
👉 γ i = d i a g ( [ K i x / L i x ] , [ K i y / L i y ] , [ K i z / L i z ] , [ K i ψ / L i ψ ] ) ∈ R 4 × 4 \boldsymbol{\gamma_i}= diag ([K_{ix}/L_{ix}],[K_{iy}/L_{iy}],[K_{iz}/L_{iz}],[K_{i\psi}/L_{i\psi}])\in\mathbb{R}^{4\times4} γi=diag([Kix/Lix],[Kiy/Liy],[Kiz/Liz],[Kiψ/Liψ])∈R4×4;
👉 K i K_{i} Ki和 L i L_{i} Li是相关的增益和延迟
- 机体系到地球系的旋转矩阵:
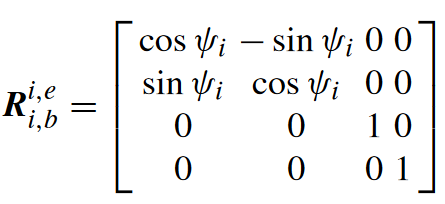
问题
🔨物理约束 ∥ τ i ∥ ∞ ≤ τ max \|\tau_i\|_\infty\leq\tau_{\max} ∥τi∥∞≤τmax
🎯目标1:当达到预设的转移时间 T i , a T_{i,a} Ti,a时,集群从跟踪编队变成包围编队。
🎯目标2:防碰撞
【这个假设感觉有点太强了;可以看出还是一个跟踪优化问题,并不是一个规划问题】
-
N+1号无人机的参考状态: Y d = [ Y d x , Y d y , Y d z , Y d ψ ] T = [ x r , y r , z r , ψ r ] T \mathcal{Y}_{d}=[\mathcal{Y}_{dx},\mathcal{Y}_{dy},\mathcal{Y}_{dz},\mathcal{Y}_{d\psi}]^{\mathrm{T}}=[x_{r},y_{r},z_{r},\psi_{r}]^{\mathrm{T}} Yd=[Ydx,Ydy,Ydz,Ydψ]T=[xr,yr,zr,ψr]T
-
编队误差
👉 M i M_i Mi 表示第 i i i台无人机相对于N+1号的距离
👉 G i G_i Gi是平滑移位函数(smooth shifting function),通过引入 G i G_i Gi和 G j G_j Gj,实现了从跟踪编队到包围编队的转换过程。具体切换公式如下:
👉注意参数 h i h_i hi是负的,这一项参数决定编队距离, δ i \delta_{i} δi决定收敛速度,越大两个状态切换时的收敛速度就越慢
-
防碰撞(与障碍物和与无人机)
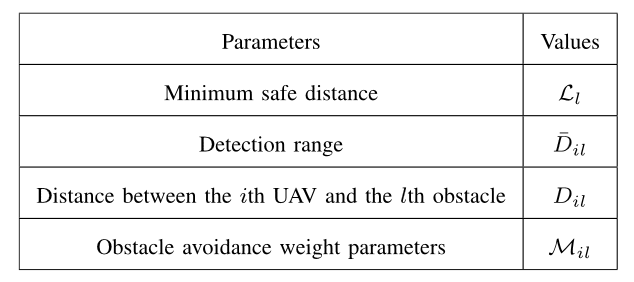
🎯与障碍物
l l l表示第 l l l个障碍物,当 D ˉ i l > D i l \bar{D}_{il}>{D_{il}} Dˉil>Dil 表示没有碰撞的风险,如果≤则碰撞的可能性直线上升
🎯与无人机
算法设计 - LMPC
- 成本函数
- 约束
很常规的MPC,主要是(16)的设计是如何保证系统稳定性的
辅助控制器 η i \eta_{i} ηi
目标:设计控制器收敛 S i , 2 S_{i,2} Si,2,使得 S i , 1 S_{i,1} Si,1稳定
-
对编队误差项求导
-
选取李雅普诺夫函数
-
求导并带入编队误差项的导
-
辅助控制器设计
η i = − γ i − 1 β i V i + γ i − 1 ( R i , b i , e ( ψ i ) ) T ( d i + b i ) ( ( d i + b i ) G ¨ i + b i Y ¨ d − ( d i + b i ) R ˙ i , b i , e ( ψ i ) V i + ∑ j ∈ N i a i , j ( R ˙ j , b j , e ( ψ j ) V j + R j , b j , e ( ψ j ) V ˙ j − G ¨ j ) + ( k i , 1 + k i , 2 ) S i , 2 + ( 1 − k i , 1 2 ) S i , 1 \begin{aligned}\eta_{i}&=-\boldsymbol{\gamma}_i^{-1}\boldsymbol{\beta}_i\boldsymbol{V}_i+\frac{\boldsymbol{\gamma}_i^{-1}\left(\boldsymbol{R}_{i,b}^{i,e}(\psi_i)\right)^\mathrm{T}}{(d_i+b_i)}\Big((d_i+b_i)\ddot{\boldsymbol{G}}_i\\&+b_i\ddot{\mathcal{Y}}_d-(d_i+b_i)\dot{\mathcal{R}}_{i,b}^{i,e}(\psi_i)\mathcal{V}_i+\sum_{j\in N_i}a_{i,j}\Big(\dot{R}_{j,b}^{j,e}(\psi_j)\mathcal{V}_j+R_{j,b}^{j,e}(\psi_j)\dot{\mathcal{V}}_j-\ddot{G}_j\Big)\\&+(k_{i,1}+k_{i,2})S_{i,2}+\left(1-k_{i,1}^2\right)S_{i,1}\end{aligned} ηi=−γi−1βiVi+(di+bi)γi−1(Ri,bi,e(ψi))T((di+bi)G¨i+biY¨d−(di+bi)R˙i,bi,e(ψi)Vi+j∈Ni∑ai,j(R˙j,bj,e(ψj)Vj+Rj,bj,e(ψj)V˙j−G¨j)+(ki,1+ki,2)Si,2+(1−ki,12)Si,1
则 V i , 2 V_{i,2} Vi,2的导数可以重写为
令 V i , L M P C = V i , 2 V_{i,LMPC} = V_{i,2} Vi,LMPC=Vi,2
😫【tbc】递归和稳定性证明
Q4 What’s the Contribution
- 构造了一个平稳的过渡函数,基于原有的通信拓扑而无需切换通信拓扑
- 设计的综合防撞算法可以应用于3D(这算啥子贡献
- 基于反推设计了一个辅助控制器作为约束,继承了反步控制器的稳定性特性,并在反步可行解的范围内寻求最优解。
Q5 What’s the Inspiration:个人的启发,Creation和畅想。
- 这个问题的难点可以拆分成三块:避障 + 跟踪 + 编队;本文用的MPC方法是把这三项都加在成本项里,用基于反推设计的辅助控制器作为李雅普诺夫约束保证稳定性。
- 缺点:计算速度估计很慢,要用非线性求解器,而且把避障加入成本项是会有可能产生碰撞的。
- 用我的模型尝试复现一下
-
-
- 👉
p
i
=
[
x
i
,
y
i
,
z
i
,
ψ
i
]
T
∈
R
4
p_i=[x_i,y_i,z_i,\psi_i]^\mathrm{T}\in\mathbb{R}^4
pi=[xi,yi,zi,ψi]T∈R4是xyz三维位置+偏航角,
-
Υ
ˉ
+
B
ˉ
\bar{\boldsymbol{\Upsilon}}+\bar{\boldsymbol{B}}
Υˉ+Bˉ是非奇异的
-
- LMPC;构造一个平稳的过渡函数, 将避障函数引入成本项,基于反推设计(backstepping)设计了辅助控制器
η
i
\eta_{i}
ηi 作为约束保证闭环稳定性
- 存在缺陷:仅考虑单个障碍物、集中式的拓扑通信,缺少用LMPC框架解决无人机在具有多个障碍物场景的跟踪包围问题。
- MPC:
- 编队控制:滑膜 \ PID \ MPC \ backstepping control
- 无障碍物场景