【数学建模】机器人避障问题
已知:
- 正方形5的左下顶点坐标 ( 80 , 60 ) (80,60) (80,60),边长 150 150 150
- 机器人与障碍物的距离至少超过 10 10 10个单位
- 规定机器人的行走路径由直线段和圆弧组成,其中圆弧是机器人转弯路径。
- 机器人不能折线转弯,转弯路径由与直线路径相切的一段圆弧组成,也可以由两个或多个相切的圆弧路径组成,但每个圆弧的半径最小为 10 10 10个单位。
- 机器人直线行走的最大速度为 v 0 v_0 v0= 5单位/秒
- 机器人转弯时,最大转弯速度为
v
=
v
(
p
)
=
v
0
/
(
1
+
e
10
−
0.1
p
2
)
v = v(p) = v_0 /( {1+ e^{10-0.1p^2}})
v=v(p)=v0/(1+e10−0.1p2)
其中 p p p是转弯半径。如果超过该速度,机器人将发生侧翻,无法完成行走。
- A点坐标 ( 300 , 300 ) (300,300) (300,300)
需要研究的问题
- 问题:机器人从 O ( 0 , 0 ) O(0,0) O(0,0)出发,到达A的最短时间及其路径
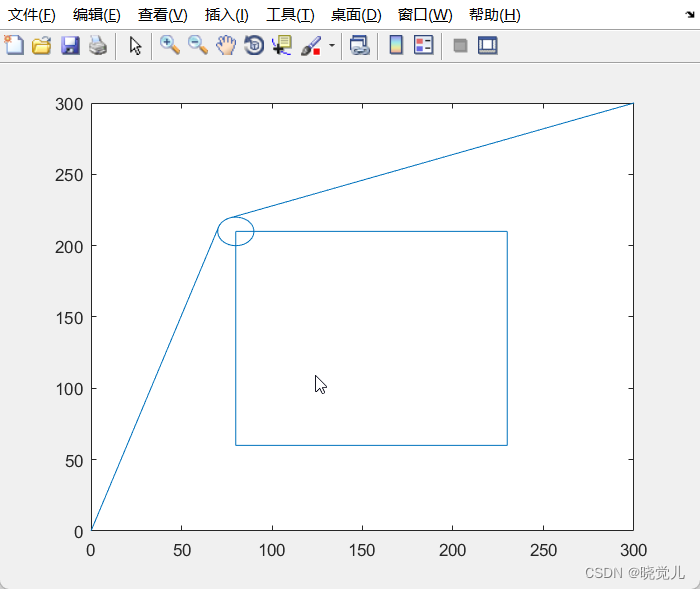
- 问题1:画出机器人只在正方形左上角拐弯,拐弯半径为10的图
- 问题2:机器人只在正方形左上角拐弯,拐弯半径为10,求路径长度和时间
- 问题3:求出最短时间及其路径
问题:机器人从 O ( 0 , 0 ) O(0,0) O(0,0)出发,到达A的最短时间及其路径
问题1:画出机器人只在正方形左上角拐弯,拐弯半径为10的图
第一问其实是为整个问题服务的 , 也算是先进行一个预测,写一个样例先
MATLAB
基本数据定义:
x = 80; y = 210; r = 10; theta = 0:pi/20:2*pi; %角度[0,2*pi] hold on;
画一个正方形:
%定义x,y轴范围 xlim([0,300]); ylim([0,300]); %四条线形成一个正方形 line([80,80],[60,210]); line([80,230],[210,210]); line([80,230],[60,60]); line([230,230],[60,210]);
在正方形左上角为圆心画圆
plot(x+r*cos(theta),y+r*sin(theta),'-');
接着求切点
建立切点模型:
设切点为 ( x 1 , x 2 ) (x_1,x_2) (x1,x2) , 正方形左上角为圆心 ( x , y ) , x = 80 ; y = 210 ; (x,y) , x = 80;y = 210; (x,y),x=80;y=210; 圆半径 r = 10 r = 10 r=10 ;切线上除切点另外一点 ( x 2 , y 2 ) (x_2,y_2) (x2,y2) ;
即圆外一点 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)引两条切线方程
因为切线和切点到圆心的直线垂直
则有 ( x − x 2 ) 2 + ( y − y 2 ) 2 = r 2 + ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 (x-x_2)^2+(y-y_2)^2 = r^2 + (x_1-x_2)^2 + (y_1-y_2)^2 (x−x2)2+(y−y2)2=r2+(x1−x2)2+(y1−y2)2
并且切点在圆上有: ( x 1 − x ) 2 + ( y 1 − y ) 2 = r 2 (x_1-x)^2 + (y_1-y)^2 = r^2 (x1−x)2+(y1−y)2=r2
由切点模型和圆外一点 O ( 0 , 0 ) O(0,0) O(0,0)建立方程求解
%这里在命令行窗口求解即可 solve('(px-80)^2+(py-210)^2=100','px^2+py^2+100=210^2+80^2');排除不符合要求的点
px = 8064/101 - (252*14^(1/2))/101; %(252*14^(1/2))/101 + 8064/101 %8064/101 - (252*14^(1/2))/101 py = (96*14^(1/2))/101 + 21168/101; %21168/101 - (96*14^(1/2))/101 %(96*14^(1/2))/101 + 21168/101
由切点模型和圆外一点 A ( 300 , 300 ) A(300,300) A(300,300)建立方程求解
%这里在命令行窗口求解即可 solve('(px-80)^2+(py-210)^2=100','(px-300)^2+(py-300)^2+100=220^2+90^2')排除不符合要求的点
px2 =9084/113 - (36*141^(1/2))/113; %(36*141^(1/2))/113 + 9084/113 %9084/113 - (36*141^(1/2))/113 py2 =(88*141^(1/2))/113 + 23748/113; %23748/113 - (88*141^(1/2))/113 %(88*141^(1/2))/113 + 23748/113
将切线画出来
line([0,px],[0,py]); line([px2,300],[py2,300]);
问题2:机器人只在正方形左上角拐弯,拐弯半径为10,求路径长度和时间
由问题一的图可知,路径分三段
先求最简单的两段直线长度
pdist([[0,0];[px,py]],'euclidean') pdist([[300,300];[px2,py2]],'euclidean') %直线总距离 L2 = pdist([[0,0];[px,py]],'euclidean') + pdist([[300,300];[px2,py2]],'euclidean');
机器人走直线时间
ans1 = L2/v0
再求弧线长度和机器人走弧度时间以及总时间
已知圆上弧长公式为: l = ∣ θ ∣ r , ( θ 为圆心角,弧度 ) l=|\theta|r , (\theta为圆心角,弧度) l=∣θ∣r,(θ为圆心角,弧度)
建立圆上两点弧长模型:
设圆上两点分别为 ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_1,y_1),(x_2,y_2) (x1,y1),(x2,y2)
则弦长为 d = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 d= \sqrt{(x_1-x_2)^2+(y_1-y_2)^2} d=(x1−x2)2+(y1−y2)2
设圆心角为 θ \theta θ,则圆周角为 θ / 2 \theta/2 θ/2
连接两点,连接其中一点和圆心并且延长 交圆上一点 ( x 3 , y 3 ) (x_3,y_3) (x3,y3) ,连接 ( x 3 , y 3 ) (x_3,y_3) (x3,y3)和另外一点,构成直角三角形
可得 s i n ( θ / 2 ) = d / ( 2 r ) sin(\theta/2) = d / (2r) sin(θ/2)=d/(2r)
所以 θ = 2 ∗ arcsin ( d / ( 2 r ) ) \theta = 2*\arcsin{(d/(2r))} θ=2∗arcsin(d/(2r))
弧长 l = θ ∗ r l = \theta * r l=θ∗r
%求弧度 %圆心角 d=sqrt((px-px2)^2+(py-py2)^2); therta=2*asin(d/20); %弧长 L=10*therta;
总时间
%求弧度 %圆心角 d=sqrt((px-px2)^2+(py-py2)^2); therta=2*asin(d/20); %弧长 L=10*therta; %直线总距离 L2 = pdist([[0,0];[px,py]],'euclidean') + pdist([[300,300];[px2,py2]],'euclidean'); v0 = 5; vp = v0/(1+(exp(1)^(10-0.1*10*10))); ans1 = L2/v0 + L/vp;
求得为 96.017639004032700
问题3:求出最短时间及其路径
由前两问我们得出了圆上两点弧长模型和建立切点模型
这一问就是结合上面模型,求一个求最小值的最优模型
设直线总长度为 s 1 s_1 s1,弧线总长度为 s 2 s_2 s2
有 min a n s = s 1 / v 0 + s 2 / v \min{ans = s_1/v0 + s_2/v} minans=s1/v0+s2/v
最优的话拐弯半径和圆心肯定会变化
设转弯圆心为 ( x , y ) (x,y) (x,y),半径为 r r r
分别以 ( 0 , 0 ) 和 ( 300 , 300 ) (0,0)和(300,300) (0,0)和(300,300)为圆外一点的切点分别为 ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_1,y_1),(x_2,y_2) (x1,y1),(x2,y2)
由建立切点模型我们可得以下方程
{ x 2 + y 2 = r 2 + x 1 2 + y 1 2 ( x 1 − x ) 2 + ( y 1 − y ) 2 = r 2 ( x − 300 ) 2 + ( y − 300 ) 2 = r 2 + ( x 1 − 300 ) 2 + ( y 1 − 300 ) 2 ( x 2 − x ) 2 + ( y 2 − y ) 2 = r 2 \begin{cases} x^2+y^2 = r^2 + x_1^2 + y_1^2 \\ (x_1-x)^2 + (y_1-y)^2 = r^2 \\ (x-300)^2+(y-300)^2 = r^2 + (x_1-300)^2 + (y_1-300)^2\\ (x_2-x)^2 + (y_2-y)^2 = r^2 \end{cases} ⎩ ⎨ ⎧x2+y2=r2+x12+y12(x1−x)2+(y1−y)2=r2(x−300)2+(y−300)2=r2+(x1−300)2+(y1−300)2(x2−x)2+(y2−y)2=r2
由圆上两点弧长模型和上述切点 ( x 1 , y 1 ) , ( x 2 , y 2 ) (x_1,y_1),(x_2,y_2) (x1,y1),(x2,y2)可得方程
s 2 = 2 ∗ ( arcsin ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 / ( 2 r ) ) ∗ r s_2 = 2 * (\arcsin{\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}/(2r)})*r s2=2∗(arcsin(x1−x2)2+(y1−y2)2 /(2r))∗r
由圆心之间可得直线距离方程
s 1 = x 2 + y 2 − r 2 / v + ( x − 300 ) 2 + ( y − 300 ) 2 − r 2 / v s_1 = \sqrt{x^2+y^2-r^2}/v + \sqrt{(x-300)^2+(y-300)^2-r^2}/v s1=x2+y2−r2 /v+(x−300)2+(y−300)2−r2 /v
或者有上述切点可得直线距离方程为
s 1 = x 1 2 + y 1 2 / v + ( x 2 − 300 ) 2 + ( y 2 − 300 ) 2 / v s_1 = \sqrt{x_1^2+y_1^2}/v + \sqrt{(x_2-300)^2+(y_2-300)^2}/v s1=x12+y12 /v+(x2−300)2+(y2−300)2 /v
由于在左上角的时候是极限情况,圆心连接正方形左上角并延长出去距离必须大于等于10可得
r − ( x − 80 ) 2 + ( y − 210 ) 2 ≥ 10 r - \sqrt{(x-80)^2 + (y-210)^2}\ge10 r−(x−80)2+(y−210)2 ≥10
LINGO求解
data: v0 = 5; e = 2.71828; enddata s = 2*r * @asin(@sqrt((x1-x2)^2 + (y1-y2)^2)/(2*r)); v = v0 / (1+e^(10-0.1*r^2)); min = @sqrt(x^2 + y^2 - r^2)/5 + @sqrt((x-300)^2 + (y-300)^2 - r^2 )/5 + s/v; x1^2 + y1^2 + r^2 = x^2 + y^2; (x2 - 300)^2 + (y2-300)^2 + r^2 = (x-300)^2 + (y-300)^2; (x1-x)^2 + (y1-y)^2 = r^2; (x2-x)^2 + (y2-y)^2 = r^2; r-@sqrt((x-80)^2+(y-210)^2)>=10; x1210; x>=80 ; x=60; y