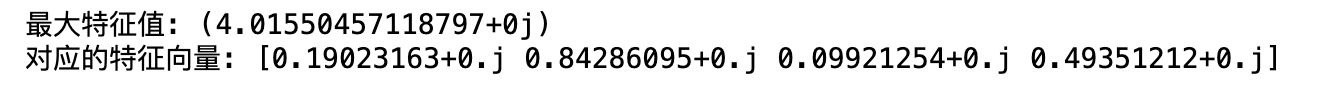python 层次分析（AHP）
文章目录
- 一、算法原理
- 二、案例分析
- 2.1 构建指标层判断矩阵
- 2.2 求各指标权重
- 2.2.1 算术平均法（和积法）
- 2.2.2 几何平均法（方根法）
- 2.3 一致性检验
- 2.3.1 求解最大特征根值
- 2.3.2 求解CI、RI、CR值
- 2.3.3 一致性判断
- 2.4 分别求解方案层权重向量及一致性检验
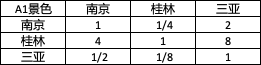
- 2.4.1 景色
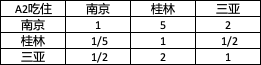
- 2.4.2 吃住
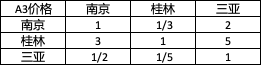
- 2.4.3 价格
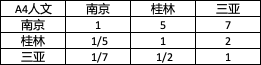
- 2.4.4 人文
- 2.5 计算各方案得分
- 三、python 代码
- 3.1 和积法计算权重
- 3.2 方根法计算权重
- 3.3 python库 np.linalg.eig
一、算法原理
-
层次分析法（analytic hierarchy process），简称AHP，是指将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初，在为美国国防部研究"根据各个工业部门对国家福利的贡献大小而进行电力分配"课题时，应用网络系统理论和多目标综合评价方法，提出的一种层次权重决策分析方法。
-
传统定性分析方法类似专家打分、专家判断等，仅能将指标简单地划分为几个层级（类似非常重要、比较重要、一般、比较不重要、非常不重要），这样导致部分存在差别但是不大的指标得到了同样的权重，受主观因素影响，无法对最终决策做出更好的帮助。层次分析法将不同指标间一一比对，主观与客观相结合，很好地解决了以上问题。
-
判断矩阵量化值参照表：
因素i比因素j 量化值 同等重要 1 稍微重要 3 较强重要 5 强烈重要 7 极端重要 9 两相邻判断的中间值 2，4，6，8 倒数 假设因素i相比因素j重要程度量化值为3，相反就是1/3 二、案例分析
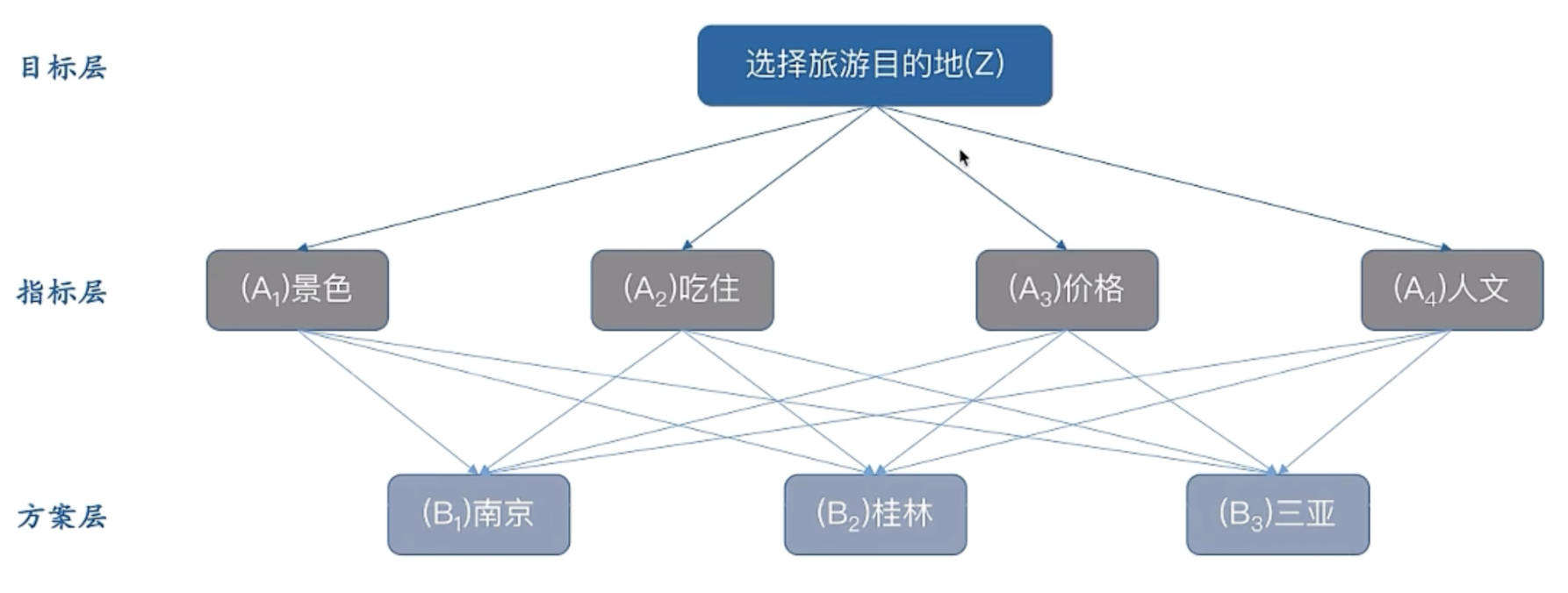
目的：选择某个城市旅游
方案：南京、桂林、三亚
考虑因素：景色、吃住、价格、人文
2.1 构建指标层判断矩阵
构建判断矩阵，理论上需要专家打分。
2.2 求各指标权重
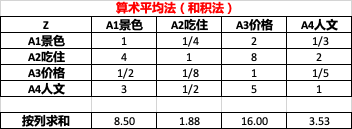
2.2.1 算术平均法（和积法）
-
按列求和：如 1 + 4 + 1 / 2 + 3 = 8.5 1+4+1/2+3 = 8.5 1+4+1/2+3=8.5。
-
将指标层判断矩阵按列归一化（即按列求占比），如：
0.12 = 1 / 8.5 0.12 = 1 / 8.5 0.12=1/8.5
0.47 = 4 / 8.5 0.47 = 4 / 8.5 0.47=4/8.5
0.06 = 1 / 2 / 8.5 0.06 = 1/2 / 8.5 0.06=1/2/8.5
0.35 = 3 / 8.5 0.35 = 3 / 8.5 0.35=3/8.5
-
将归一化后的矩阵按行求平均，得到权重向量w
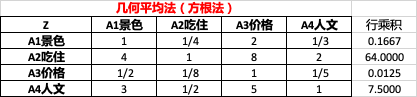
2.2.2 几何平均法（方根法）
-
每行各元素相乘（行乘积），如 1 ∗ 1 / 4 ∗ 2 ∗ 1 / 3 = 0.1667 1*1/4*2*1/3 = 0.1667 1∗1/4∗2∗1/3=0.1667
-
对乘积列每个元素开n次方（n为矩阵阶数，此处n=4），如 0.1667 4 = 0.6389 \sqrt[4]{0.1667}=0.6389 40.1667 =0.6389.
-
然后对开方列求列占比，得到权重向量w，如 0.1171 = 0.6389 / 5.4566 0.1171=0.6389 / 5.4566 0.1171=0.6389/5.4566.
2.3 一致性检验
2.3.1 求解最大特征根值
得到权重向量后，可以计算出原判断矩阵的最大特征根值，公式为：
λ m a x = 1 n ∑ i = 1 n ( A W i ) W i \lambda_{max}=\dfrac{1}{n}\sum_{i=1}^{n}{\dfrac{(AW_{i})}{W_{i}}} λmax=n1i=1∑nWi(AWi)
其中，n为矩阵阶数，此处n=4。
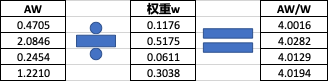
求解步骤（以和积法求解权重为例）
-
求 A W AW AW，其中 0.4705 = 1 ∗ 0.1176 + 1 4 ∗ 0.5175 + 2 ∗ 0.0611 + 1 3 ∗ 0.3038 0.4705=1*0.1176+\dfrac{1}{4}*0.5175+2*0.0611+\dfrac{1}{3}*0.3038 0.4705=1∗0.1176+41∗0.5175+2∗0.0611+31∗0.3038
-
求 A W W \dfrac{AW}{W} WAW，如 4.0016 = 0.4705 / 0.1176 4.0016=0.4705/0.1176 4.0016=0.4705/0.1176
-
求 1 n s u m ( A W W ) \dfrac{1}{n}sum(\dfrac{AW}{W}) n1sum(WAW)，此处 s u m ( A W W ) = 16.0621 sum(\dfrac{AW}{W})=16.0621 sum(WAW)=16.0621
-
综上求得 λ m a x = 1 4 ∗ 16.0621 = 4.0155 \lambda_{max}=\dfrac{1}{4}*16.0621=4.0155 λmax=41∗16.0621=4.0155。
2.3.2 求解CI、RI、CR值
- 计算CI
C I = λ − n n − 1 = 4.0155 − 4 4 − 1 = 0.0052 CI=\dfrac{\lambda-n}{n-1}=\dfrac{4.0155-4}{4-1}=0.0052 CI=n−1λ−n=4−14.0155−4=0.0052
- 计算RI
根据查表，得知 R I RI RI为0.89
- 计算CR
C R = C I R I = 0.0052 0.89 = 0.0058 CR=\dfrac{CI}{RI}=\dfrac{0.0052}{0.89}=0.0058 CR=RICI=0.890.0052=0.0058
2.3.3 一致性判断
CR = 0.0058
2.4 分别求解方案层权重向量及一致性检验
2.4.1 景色
-
构建判断矩阵
-
计算权重向量以及一致性检验.（步骤如上文，为了简便文章，本次计算采用python代码，以和积法求解权重，下文将详细介绍）
2.4.2 吃住
-
构建判断矩阵
-
计算权重向量以及一致性检验.（步骤如上文，为了简便文章，本次计算采用python代码，以和积法求解权重，下文将详细介绍）
2.4.3 价格
-
构建判断矩阵
-
计算权重向量以及一致性检验.（步骤如上文，为了简便文章，本次计算采用python代码，以和积法求解权重，下文将详细介绍）
2.4.4 人文
-
构建判断矩阵
-
计算权重向量以及一致性检验.（步骤如上文，为了简便文章，本次计算采用python代码，以和积法求解权重，下文将详细介绍）
2.5 计算各方案得分
综合得分 = s u m ( 单项得分 ∗ 对应指标权重 ) 综合得分=sum(单项得分*对应指标权重) 综合得分=sum(单项得分∗对应指标权重)
可以看出，南京得分0.5675为最高，最终方案应选择南京。
三、python 代码
3.1 和积法计算权重
import numpy as np import pandas as pd ''' 层次分析法判断矩阵权重向量计算--和积法 ''' def get_w_anc(factors_matrix): # RI字典 RI_dict = { 1:0, 2:0, 3:0.52, 4:0.89, 5:1.12, 6:1.26, 7:1.36, 8:1.41, 9:1.46, 10:1.49, 11:1.52, 12:1.54, 13:1.56, 14:1.58, 15:1.59 } # 矩阵阶数 shape = factors_matrix.shape[0] # 按列求和 column_sum_vector = np.sum(factors_matrix, axis=0) # 指标层判断矩阵归一化 normalization_matrix = factors_matrix / column_sum_vector # 按行求归一化后的判断矩阵平均值，得到权重W W_vector = np.mean(normalization_matrix, axis=1) # 原判断矩阵 乘以 权重向量 AW_vector = np.dot(factors_matrix, W_vector) # 原判断矩阵 ✖️ 权重向量 / 权重 AW_w = AW_vector / W_vector # 求特征值 lamda = sum(AW_w) / shape # 求CI值 CI = (lamda - shape) / (shape - 1) # 求CR值 CR = CI / RI_dict[shape] print("权重向量为：",list(W_vector)) print("最大特征值：",lamda) print("CI值为：",CI) print("RI值为：",RI_dict[shape]) print("CR值为：",CR) if CR- 运行结果
3.2 方根法计算权重
这里只列出计算权重部分
- 原指标层判断矩阵
# 指标层判断矩阵 factors_matrix = np.array([ [1,1/4,2,1/3], [4,1,8,2], [1/2,1/8,1,1/5], [3,1/2,5,1] ])- 求行乘积
# 求行乘积 array1 = factors_matrix.prod(axis=1, keepdims=True)
- 对乘积列每个元素开n次方（n为矩阵阶数，此处n=4）
n = 4 array2 = np.power(array1, 1/n)
- 对开方列求列占比，得到权重向量w
array2 / np.sum(array2)
3.3 python库 np.linalg.eig
# 计算特征值和特征向量 eigenvalues, eigenvectors = np.linalg.eig(factors_matrix) # 需要注意的是，对于一个nxn的矩阵，最多可能有n个特征值和特征向量，因此，需要挑选出最大的特征值进行一致性判断 # 找到最大特征值的索引 max_eigenvalue_index = np.argmax(eigenvalues) # 提取最大特征值和对应的特征向量 max_eigenvalue = eigenvalues[max_eigenvalue_index] max_eigenvector = eigenvectors[:, max_eigenvalue_index] print("最大特征值:", max_eigenvalue) print("对应的特征向量:", max_eigenvector)
- 参考：层次分析法（AHP）步骤详解-哔哩哔哩
- 参考：层次分析法原理及计算过程详解）
- 原指标层判断矩阵
-
- 计算CR
- 计算RI
-
-
