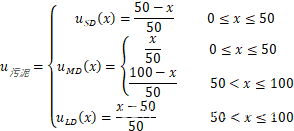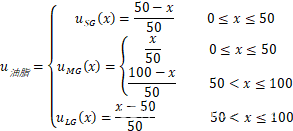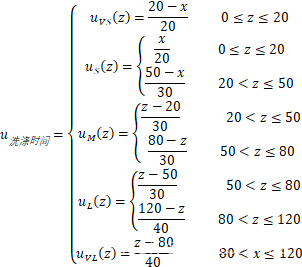【人工智能】模糊逻辑推理-洗衣机模糊推理系统
一、实验目的
理解模糊逻辑推理的原理及特点,熟练应用模糊推理,并以此设计一个洗衣机模糊推理系统。
二、实验原理
模糊推理即以模糊集合论为基础描述工具,对以一般集合论为基础描述工具的数理逻辑进行扩展,从而建立了模糊推理理论。是不确定推理的一种。在人工智能技术开发中有重大意义。
整个模糊推理的过程就是由一组模糊规则出发。许多模糊规则实际上是一组多重条件语句,可以表示为从条件论域到结论论域的模糊关系矩阵R。通过条件模糊向量与模糊关系R的合成进行模糊推理,得到结论的模糊向量,然后采用“清晰化”方法将模糊结论转换为精确量。
三、实验过程记录
已知人的操作经验为:
“污泥越多,油脂越多,洗涤时间越长”;
“污泥适中,油脂适中,洗涤时间适中”;
“污泥越少,油脂越少,洗涤时间越短”
可以得到以下模糊控制规则表
| x | y | z |
| SD | NG | VS |
| SD | MG | M |
| SD | LG | L |
| MD | NG | S |
| MD | MG | M |
| MD | LG | L |
| LD | NG | M |
| LD | MG | L |
| LD | LG | VL |
其中SD(污泥少)、MD(污泥中)、LD(污泥多)、NG(油脂少)、MG(油脂中)、LG(油脂多)、VS(洗涤时间很短)、S(洗涤时间短)、M(洗涤时间中等)、L(洗涤时间长)、VL(洗涤时间很长)。
假设污泥、油脂、洗涤时间的论域分别为[0,100]、[0,100]、[0,120],设计模糊推理系统如下:
输入:待洗涤衣物的污泥和油脂
控制对象:洗涤时间
污泥隶属函数:
油脂隶属函数:
时间隶属函数:
Python代码实现:
def Sludge(a):#污泥
sludge=[0,0,0]#默认隶属度为0,依次对应SD,MD,LD
if a100:
return (print("输入值有误"))
elif 0