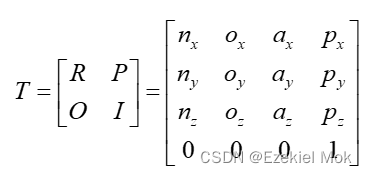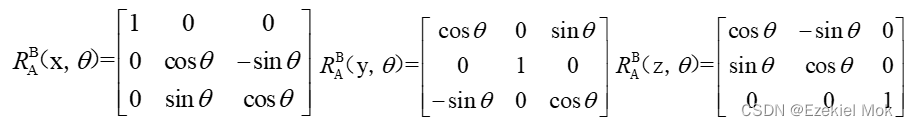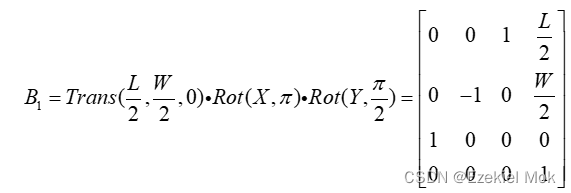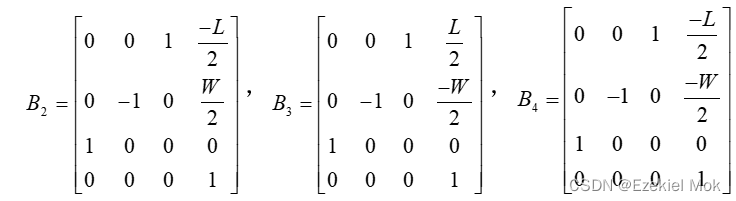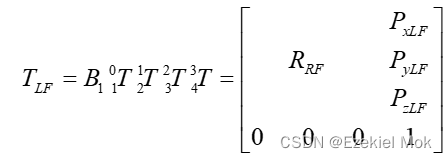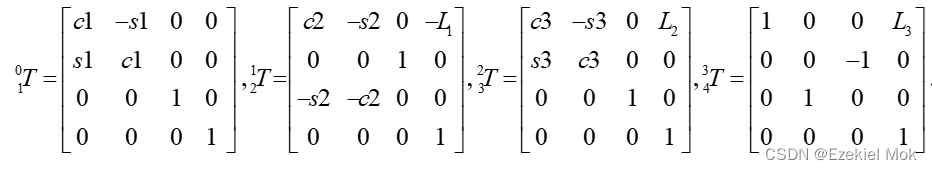相对全面的四足机器人驱动规划MATLAB和Simulink实现方式(足端摆线规划,Hopf-CPG,Kimura-CPG)
许久没更新四足机器人相关的博客文章,由于去年一整年都在干各种各样的~活,终于把硕士毕业论文给写好,才有点时间更新自己的所学和感悟。步态规划和足端规划只是为了在运动学层面获取四足机器人各关节的期望角位移和速度信号,再由底层的关节控制器输出控制律(角加速度或力矩)使得期望和现实信号的偏差在容许范围内,今天将来探讨下四足机器人的三种常见的驱动方式,并用数值仿真和simscape仿真的方式验证所提出方法的有效性,对比其优缺点。
图1. 四足机器人simscape实时交互仿真
1. 四足机器人步态定义
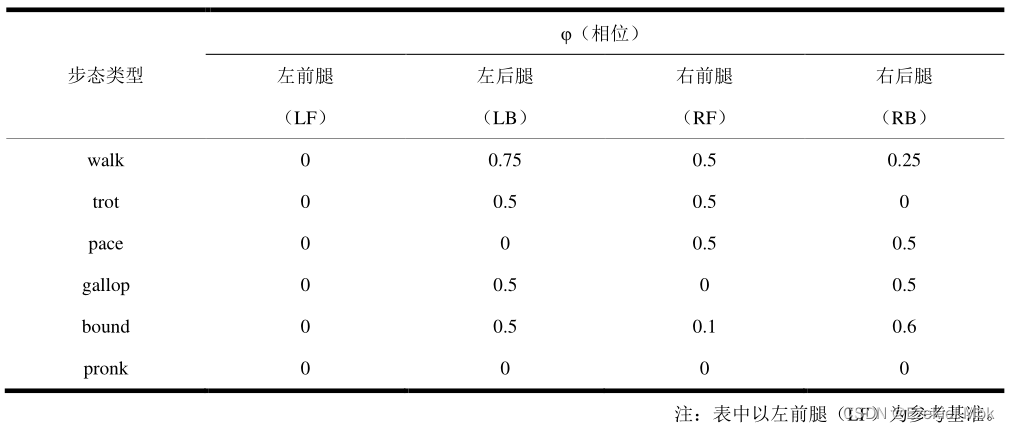
依据文献[8],四足动物的步态是指各个腿之间具有固定相位关系的行走模式,不同的动物由于自身条件的限制,如腿长、腿的位置、神经控制方式等,其步态也会变得不一样。就如双足动物的“行走”、“奔跑”,四足动物的行走(Walk)、对角小跑(Trot)、奔跑(Gallop)、溜步(Pace)、跳跑(Bound)、原地四足跳跃(Pronk)。以 LF(左前腿)、RF(右前腿)、RB(右后腿)、LB(左后腿)分别替代四足动物的四条腿,然后可以根据其步态的特点得出它们各自的相位关系(左前腿作为参考基准,φ_LF=0 ,即相位为0,一个周期为2*pi ),以上步态的相位关系如表1所示。 步态是实现仿生四足机器人运动性能的基础规划,步态的协调性、连续性与可调整性直接决定着仿生四足机器人运动性能的优劣。
表1. 各种步态相位关系
步态可以由特定的几个参数表征,相位差φ_i 、负载因子β、步态周期T、步长S、抬腿高度h,定义一个步态周期T内,腿部离地的时间被称为摆动相,撑地的时间称为支撑相,具体参数有以下定义:
表2. 机器人步态参数定义
通过对四足动物的运动观察与分析,总结出了四足动物的步态描述表,其中的节奏可以分为单拍、双拍、准双拍、四拍步态,可以从四足动物足端拍打地面的节拍进行区分,例如Trot是双拍步态,Walk是四拍步态。另外,负载因子(步态占空比)β衡量腿部与地面的接触时间与步态周期的比重,有着重要的意义,因为当β等于0.5时,机器人在任意时刻或者平均约有两条腿支撑地面,而当β大于或者等于0.5的时候,说明机器人在任意时刻或者平均至少有三条腿支撑地面,这对机器人的步态输出有着极其重要的作用。其中,walk 步态β值为 0.75,trot 和其余常规步态的β为0.5。
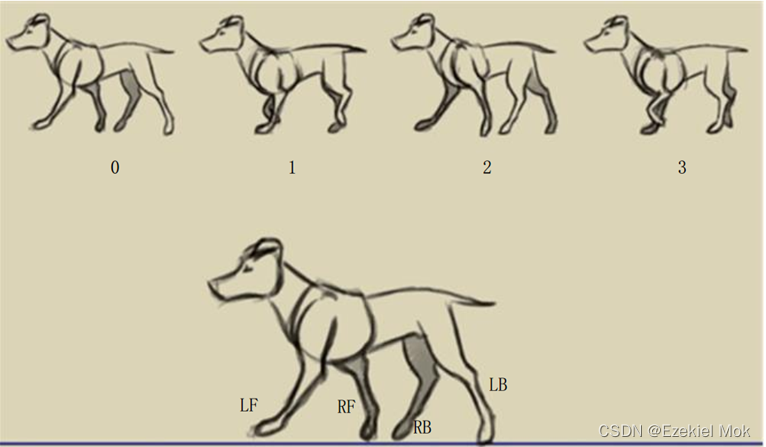
图1.四足动物行走步态示意
如图1所示,四足机器人起步时,左前腿LF抬起后以一定的足端轨迹向前跨步,待LF落地后紧跟着右后腿RB跨腿,之后再轮到RF、LB进行相同的动作,行走的过程中,该动作重复循环,步态周期较长并且在走动的过程始终保持三条腿在支撑身体。而小跑步态,先是LF与RB同时抬起并同步抬腿运动,当LF与RB重新落到地面时候,RF与LB跨腿,重复循环,为身体保持平稳,步态周期较短,在小跑过程中的任意时刻都只有对角腿在支撑身体,具体的相位拓扑关系分析见我的另一个文章EzekielMok。
2. 单腿正-逆向运动学计算
要实现四足机器人的精准控制,需获取精确的关节角度空间下的角位移-角速度-角加速度与笛卡尔坐标下足端的位置-速度-加速度之间的映射关系,不同腿部结构的四足机器人的映射关系不一样,如有些是串联式的多关节机械臂,某些是并联式的机械臂,它们都可依据机器人学[1]的建模方法求解分析。
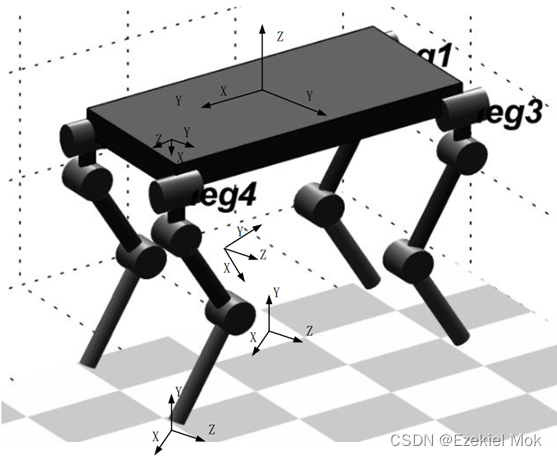
图2.四足机器人机身坐标定义
2.1 正向运动学分析
根据机器人学[1]中的连杆上坐标系建模原则进行坐标变换,可以推导出一个包含姿态信息与位置信息的齐次矩阵
其中,R为旋转矩阵,表征位姿变换;P为位置矩阵,表征位置变换;O是透视矩阵,此处元素全为0;I是比例变换矩阵,没有长度变化的情况下为1;n=[nx,ny,nz],n=[ox,oy,oz],n=[ax,ay,az]表示相对坐标系X,Y,Z参考坐标系的方向余弦;在R矩阵中每一步变换,有三种变换方式,即是分别绕X、Y、Z轴旋转相应的角度。现定A为参考坐标系,B为变换目标的相对坐标系,θ表示变换的转角,根据正交原则有如下的变换矩阵:
有了以上的机器人学建模分析基础后,将图所示常见机构简化为以下图所示的机身腿节坐标分析模型。
图3.四足机器人抽象关节坐标定义
定义机身坐标如图3所示,其中机身前进方向为X,左右侧移方向为Y,高度方向为Z,假设侧摆关节之间的距离W,前后髋关节之间的距离L,机器人三个腿节长度L1、L2、L3。并以此为分析基点,分析四足机器人单腿的正-逆向运动学分析。采用机器人学应用最广泛的建模方法DH(Denavit-Hartenberg)方法[1],重要的两个建模原则是:1.对于笛卡尔坐标系,第i+1旋转关节的轴线方向始终指向Zi轴的正方向;2.对于笛卡尔坐标系,尽量把连杆的方向定为X轴的正向,即是Xi坐标的轴沿着Zi与Zi-1的公垂线,且指向Zi-1轴的负方向。
四足机器人机身的中心为坐标基点到左前腿LF的过渡矩阵B1的变换矩阵推导如下:
其中,Trans(·)为坐标系的平移变换矩阵公式,Rot(·)为旋转变换公式,L为机器人机体的长度,W为机体的宽度。同理推导得其他三个腿的过渡变换矩阵为
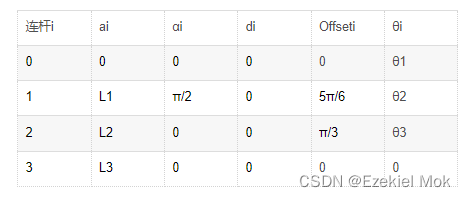
定义机身的中心为坐标基点,以左前腿为例,依据机器人学的DH建模法给出连杆参数如下:
表3. 单腿连杆DH参数定义
其中,ai是沿着xi方向,从zi到zi+1平移的距离;αi是绕着xi方向,从zi到zi+1转过的角度;di 是沿着zi方向,从xi-1到xi平移的距离,θi是绕着zi 方向,从xi-1到xi 转过的角度。Offseti是第i个关节的补偿值,作为初始姿态角。因此,机身中心到左腿足端的坐标变换矩阵定义为
其中,
式子中, s1=sin(θ1),c1=cos(θ1),s2=sin(θ2),c2=cos(θ2),s3=sin(θ3),c3=cos(θ3)。
单腿正向向运动学计算代码(此处从B1坐标系转换至足端,机身中心至B1加个矩阵就行):
function [T,R,P] = Kine(L1,L2,L3,alpha_du,beta_du,gama_du)%
%输出角度为弧度
% du_trans = 180/pi;
rad_trans = pi/180;
alpha = alpha_du*rad_trans;
beta = beta_du*rad_trans;
gama = gama_du*rad_trans;
T_01 = [[cos(alpha) -sin(alpha) 0 0];
[sin(alpha) cos(alpha) 0 0];
[0 0 1 0];
[0 0 0 1]];
T_12 = [[cos(beta) -sin(beta) 0 0];
[0 0 0 L1];
[-sin(beta) -cos(beta) 1 0];
[0 0 0 1]];
T_23 = [[cos(gama) -sin(gama) 0 L2];
[sin(gama) cos(gama) 0 0];
[0 0 1 0];
[0 0 0 1]];
T_34 = [[1 0 0 L3];
[0 1 0 0];
[0 0 1 0];
[0 0 0 1]];
%% 正向运动学矩阵
T = T_01*T_12*T_23*T_34;%% 可以通过替换参数直接求取结果
R = T(1:3,1:3);
P = T(1:3,4);
end
至此,正向运动学求解完毕,可实现关节空间到笛卡尔空间的映射计算。
2.2 逆向运动学分析
逆向运动学分析为了获取笛卡尔空间至关节空间的映射关系,可以通过期望的足端轨迹给定期望的关节角位移、角速度和角加速度期望控制量,是做四足机器人行为和稳定性控制的重要基础,具体方法包括几何求解法和解析解法。 以下将参考文献[2][3],利用几何解析法来求解单腿的逆向运动学。
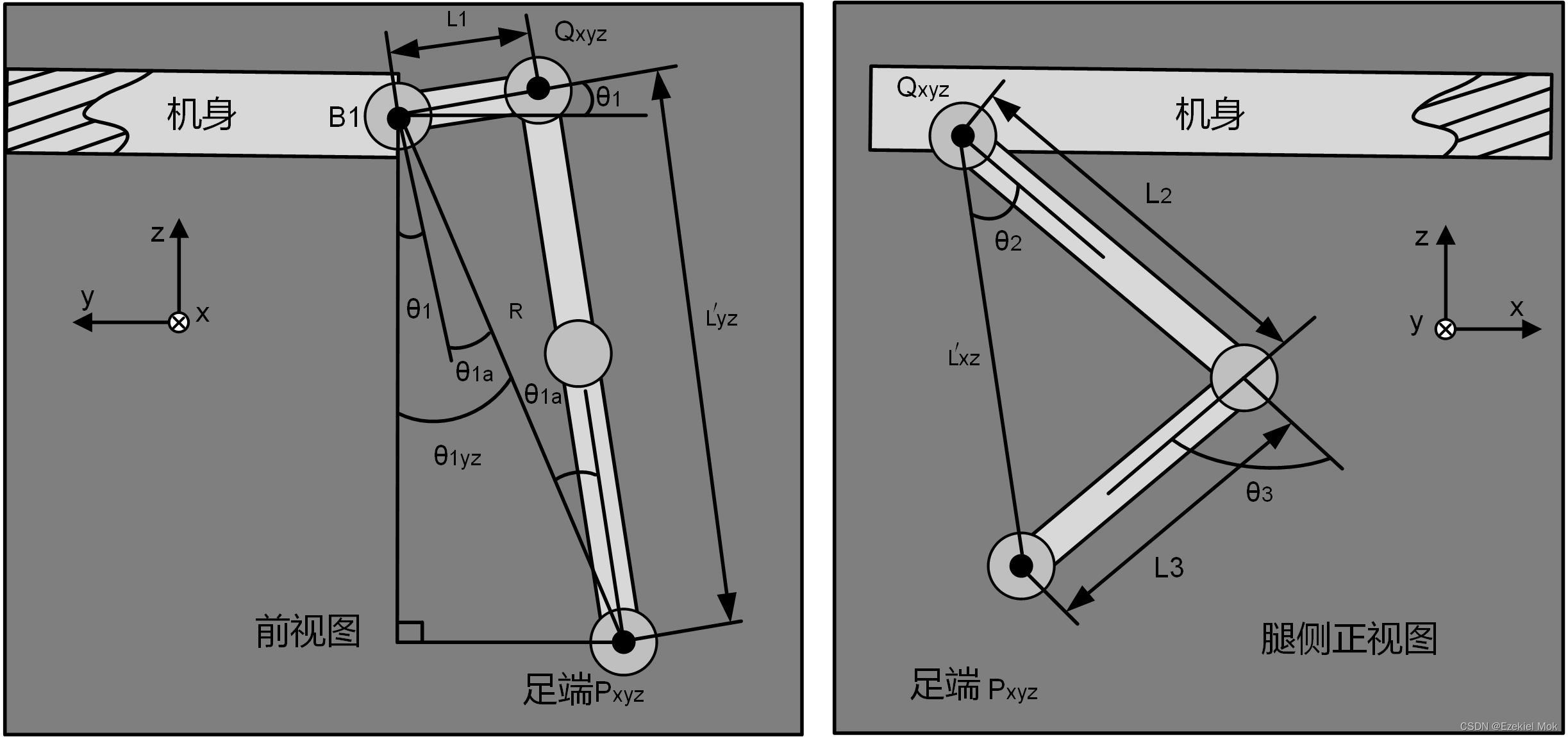
图4.四足机器人侧视和前视图
如图4所示,θ1是侧摆角,绕X轴旋转,最大旋转角度约束为20度,初始转角为0度(初始站立姿态的转角);θ2是髋关节转角,最大旋转关节角度约束为
35度(我自己simscape仿真里给定的,根据自己具体工况设计),初始转角为45度;θ3为膝关节转角,最大旋转关节角度约束为
45度,初始转角为135度。
给定足端的期望空间位置(以机身坐标原点为起始坐标),以及连杆长度,机体长度和宽度(以腿节计算),以右手定则(图5)判定各坐标的方位和关节旋转角的正负值,利用几何法求解θ1,θ2,θ3。
图5.坐标正负方向定义右手定则(逆时针为正方向)
首先求θ1,几何关系如图6所示,简单明了,用小学初中三角函数知识便可求解,需要注意的是actan(·)的求解范围要定义好,根据上述的坐标图示可知,此处的y和z坐标均为负,由右手定则可规定θ1为负。给定足端相对侧摆关节坐标的参考坐标
,根据图中的几何关系,会有以下等式:
图6. 单腿几何关系分析图示
再者求θ3,如图7所示,腿节关系可以抽象为一个三角形,依据坐标设定,足端x方向的坐标假设为正值,根据余弦定理就可以直接求取θ2如下
最后求θ2,也依赖于上述的抽象三角形关系,θ2由θ2a和θ2b两部分构成,根据正切三角关系和余弦定理可以直接求取θ2如下
图7. 单腿几何关系分析图示
单腿逆向运动学计算代码:
%代码实现方式1
function [alfa, beta, gamma]=xyztoang(x, y, z)
h_up=49.0;
h_mid=125.5899;
h_low=116.0+20;
dyz=sqrt(y.^2+z.^2);
lyz=sqrt(dyz.^2-h_up.^2);
gamma_yz=-atan(y./z);
gamma_h_offset=-atan(h_up./lyz);
gamma=gamma_yz-gamma_h_offset;
lxzp=sqrt(lyz.^2+x.^2);
n=(lxzp.^2-h_low^2-h_mid.^2)/(2*h_mid*h_low);
beta=-acos(n);
alfa_xzp=-atan(x/lyz);
alfa_off=acos((h_mid+n)/lxzp);
alfa=(alfa_xzp+alfa_off);
end
%代码实现方式2
function [theta] = Kine_inv(L1,L2,L3,P)%
theta = zeros(3,1);
du_trans = 180/pi;
rad_trans = pi/180;
True = 1;
phai = atan2(P(2),P(1));%求角度
rlo = sqrt(P(1).^2 + P(2).^2);
rlo1 = sqrt(P(1).^2 + P(2).^2 - L1.^2);
if True
theta(1) = phai - atan2(L1, rlo1);
theta(1) = theta(1)*du_trans;
end
theta(3) = -acos((P(1).^2 + P(2).^2 + P(3).^2 - L1.^2 - L2.^2 - L3.^2)/(2*L2*L3));
theta(3) = theta(3)*du_trans;
a = P(1)*cos(theta(1)*rad_trans) + P(2)*sin(theta(1)*rad_trans);
b = -P(3);
rlo2 = sqrt(a.^2 + b.^2);
theta(2) = pi-asin((L3.^2 - L2.^2 - a.^2 - b.^2)/(-2*L2*rlo2)) - asin(a/rlo2);
theta(2) = theta(2)*du_trans;
end
至此,运动学逆解求解完毕。
3. 行走足端轨迹约束条件
通用引用四足机器人相关的文献和资料[2][3][4][7],要实现足式机器人理想的步态行走,其足端的空间轨迹需要满足:
- 1. 行进平稳和协调,无明显的上下波动、左右摇晃和前后冲击;
- 2. 各关节在摆动相抬腿和落地瞬间无较大冲突,可以无冲击抬腿和平滑落地;
- 3. 摆动相跨腿迅速,足端轨迹平滑,关节速度和加速度平滑连续无畸点;
- 4. 避免足端与地面发生滑动和拖地现象。
为了满足上述的四个要求,假定此时(为便于分析,与上述机身的整体坐标不一样,整体的坐标)的蹬腿前进方向为X,抬腿高度方向为Y,在笛卡尔空间下对给定足端轨迹状态方程施加约束条件如下:
图8. 机器人足端坐标定义
其中,
分别是X方向和Y方向的笛卡尔坐标位置,
为速度,
为加速度,S为抬腿,步长H为抬腿高度。
4.足端复合摆线规划
足端摆线规划是当前四足机器人最常见的驱动方式[2][4],如波士顿动力学spotdog,MIT,绝影,宇树、淘宝上各种无刷电机狗以及舵机狗都是采用摆线规划,可见其实用性。足端摆线规划是将四足机器人行走时候的足端运动建模成一个空间中运动的摆线,这样能够尽量减少足端在触地瞬间的爆发冲击,更好地与地面摩擦,实现机身的前进驱动。
摆线,又称旋轮线、圆滚线,在数学中,摆线(Cycloid)被定义为,一个圆沿一条直线运动时,圆边界上一定点所形成的轨迹。它是一般旋轮线的一种。标准摆线的参数方程为
其中,
表示摆线圆弧的半径,
为滚动角。摆线的MATLAB数值仿真绘制代码如下:
%Ezekiel %2023年3月25日 %% 清理变量 clc; clear; close all; n=2000; r = 1; for index = 0:1:n theta = 5*pi/1000*index; x(index+1) = r*(theta - sin(theta)); y(index+1) = r*(1 - cos(theta)); end plot (x, y,'-r','linewidth',1); axis equal grid on xlabel('X') ylabel('Y')图9. 摆线数值仿真示意
单纯的摆线能够很好地满足足端轨迹状态方程的约束条件,但是与地面接触时候存在着滑动和行为时候出现拖地的现象,因此根据文献[11]对摆线规划进行针对性设计,为复合摆线规划,其参数方程定义为
其中,S为抬腿步长,H为抬腿高度,
为摆动相时间。具体的MATLAB代码实现如下
function [X, Y] = Gait_cal(S_0,H,Ty,Tst,index1,Point_num_Tt) %% 改进的复合摆线规划 r = S_0/(2*pi); % 摆线的半径 Tt = Ty + Tst; % 计算周期长度,摆动相和支撑相 Tsa = Tt/(Point_num_Tt-1);%计算所处周期序列 n = 4; %% 摆动相与支撑相分别规划 % 取模运算 Trun = (index1 - 1)*Tsa;%时刻 if Trun >= 0 && Trun = 0 && Trun为了便于周期性输入控制接入,利用周期性的方波信号控制摆线的频率(周期),简单来说,就是利用方波的输入控制四足机器人的抬腿和落脚时间,可以通过占空比的形式直接控制摆动相和支撑相的比例,进而控制实现四足机器人各种不同的步态,具体的调制原理可见代码和simulink实现环节。
%Ezekiel %2023年3月25日 %% 清理变量 clc; clear; close all; n=2000; t_total = 6*pi/2; t=linspace(0,t_total,n);%转一圈 ts=t_total/n; trace_sq = nan+t;%轨迹配置初始化,空值 trace_xyz = nan+[t;t;t];%轨迹配置初始化,空值 trace_abg= nan+[t;t;t];%轨迹配置初始化,空值 trace_triang = nan+t;%轨迹配置初始化,空值 k=0; omega = 2*pi;% 控制步态周期 siggnal_sq_intergration1 = 0; siggnal_sq_intergration2 = 0; S = 50; H = 40; Tm = 0.5; for j=t k=k+1; singnal_sq1_1 =0.5*square(omega*j)+0.5; singnal_sq1_2 =0.5*square(omega*j/2)+0.5; singnal_sq2_1 =0.5*square(2*omega*j)+0.5; singnal_sq2_2 =0.5*square(omega*j)+0.5; siggnal_sq_intergration1 = siggnal_sq_intergration1 + ts*logic_clock(singnal_sq1_1); singnal_triang1 = siggnal_sq_intergration1*logic_clock(singnal_sq1_2); siggnal_sq_intergration2 = siggnal_sq_intergration2 + ts*logic_clock(singnal_sq2_1); singnal_triang2 = siggnal_sq_intergration2*logic_clock(singnal_sq2_2); trace_triang(k)= siggnal_sq_intergration1; x_3d = cycloid_x(singnal_triang1,Tm,S); z_3d = 150-cycloid_y(singnal_triang2,Tm,H); y_3d = 49; [alfa_dg, beta_dg, gamma_dg]=xyztoang( x_3d, y_3d, z_3d); trace_xyz(:, k)= [x_3d;y_3d;z_3d]; trace_abg(:, k)= [alfa_dg; beta_dg; gamma_dg]; trace_sq(k)= singnal_sq1_1; end subplot(4,1,1) plot(t,trace_sq(:),'red') % title('Kimura振荡器输出') ylabel('pulse') axis([0,t_total ,-0.5,1.5])%XY坐标均衡 grid on; subplot(4,1,2) plot(t,trace_triang(:),'blue') ylabel('trangpulse') axis([0,t_total ,0,1])%XY坐标均衡 grid on; subplot(4,1,3) plot(trace_xyz(1, :),trace_xyz(3, :),'red') ylabel('XY-plot') axis([0,50 ,100,160])%XY坐标均衡 grid on; subplot(4,1,4) plot(t, trace_abg(1, :), 'blue', t, trace_abg(2, :), 'red',t, trace_abg(3, :), 'green') ylabel('theta') axis([0,t_total ,-3,2])%XY坐标均衡 grid on; function y = logic_clock(u) if u==0 y = -1; else y=1; end end function x = cycloid_x(u,Tm,S) if u>0 x =S*(u/Tm-1/(2*pi)*sin(2*pi*u/Tm)); else u=-u; x =S*(u/Tm-1/(2*pi)*sin(2*pi*u/Tm)); end end function y = cycloid_y(u,Tm,H) n=4; if u>0 y=2*H*(u/Tm-1/(n*pi)*sin(n*pi*u/Tm)).*(u>=0&u=Tm/2&u0 leg_k_Point_x(n,i)=0; else if(i