算法打卡day24|回溯法篇04|Leetcode 93.复原IP地址、78.子集、90.子集II
温馨提示:这篇文章已超过426天没有更新,请注意相关的内容是否还可用!
算法题
Leetcode 93.复原IP地址
题目链接:93.复原IP地址
大佬视频讲解:复原IP地址视频讲解
个人思路
这道题和昨天的分割回文串有点类似,但这里是限制了只能分割3次以及分割块的数字大小,根据这些不同的条件用回溯法解决就好啦
解法
回溯法
把切割问题抽象为如下树形结构
回溯法三部曲
1.递归参数
这里的startIndex一定是需要的,因为不能重复分割,记录下一层递归分割的起始位置。
还需要一个变量pointNum,记录添加逗点的数量。
2.递归终止条件
本题明确要求只会分成4段,所以不能用切割线切到最后作为终止条件,而是分割的段数作为终止条件。pointNum表示逗点数量,pointNum为3说明字符串分成了4段了。然后验证一下第四段是否合法,如果合法就加入到结果集里
3.单层搜索的逻辑
在for (int i = startIndex; i
递归调用时,下一层递归的startIndex要从i+2开始(因为需要在字符串中加入了分隔符.),同时记录分割符的数量pointNum 要 +1。
回溯的时候,就将刚刚加入的分隔符. 删掉就可以了,pointNum也要-1。
判断子串是否合法
按题意看主要考虑到如下三点:
- 段位以0为开头的数字不合法
- 段位里有非正整数字符不合法
- 段位如果大于255了不合法
class Solution { List result = new ArrayList();//结果列表 StringBuilder stringBuilder = new StringBuilder();//收割子字符串 public List restoreIpAddresses(String s) { restoreIpAddressesHandler(s, 0, 0); return result; } public void restoreIpAddressesHandler(String s, int start, int number) { // number表示stringbuilder中ip段的数量 // 如果start等于s的长度并且ip段的数量是4,则加入结果集,并返回 if (start == s.length() && number == 4) { result.add(stringBuilder.toString()); return; } // 如果start等于s的长度但是ip段的数量不为4,或者ip段的数量为4但是start小于s的长度,则直接返回 if (start == s.length() || number == 4) { return; } // 剪枝:ip段的长度最大是3,并且ip段处于[0,255] for (int i = start; i = 0 && Integer.parseInt(s.substring(start, i + 1)) 1 && s.charAt(start) - '0' == 0) { continue; } stringBuilder.append(s.substring(start, i + 1)); // 当stringBuilder里的网段数量小于3时,才会加点;如果等于3,说明已经有3段了,最后一段不需要再加点 if (number时间复杂度:O(3^4);(IP地址最多包含4个数字,每个数字最多有3种可能的分割方式,则搜索树的最大深度为4,每个节点最多有3个子节点)
空间复杂度:O(n);(递归栈的深度最多为 n)
Leetcode 78.子集
题目链接:78.子集
大佬视频讲解:子集视频讲解
个人思路
这是典型的子集问题,也就是找树的所有节点,利用回溯法,将所有节点都加入结果列表。
解法
回溯法
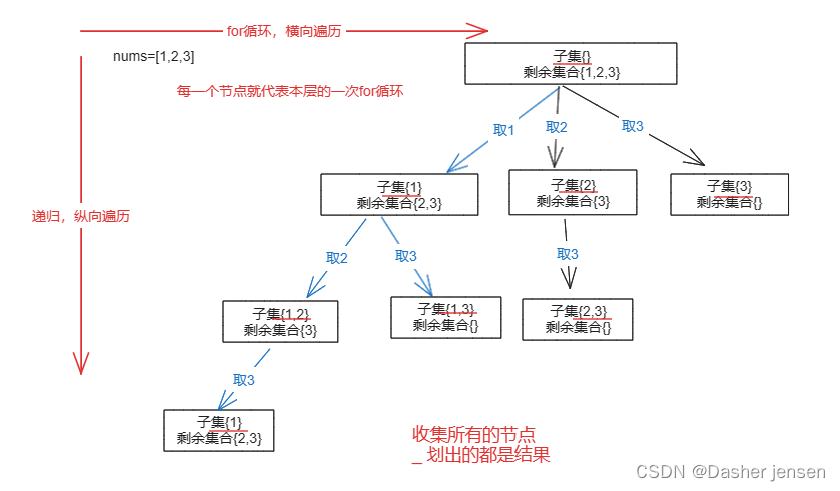
把求子集问题抽象为如下树形结构:
从图中红线部分,可以看出遍历这个树的时候,把所有节点都记录下来,就是要求的子集集合。
回溯法三部曲
子集也是一种组合问题,因为它的集合是无序的,子集{1,2} 和 子集{2,1}是一样的。
1.递归函数参数
全局变量数组path为子集收集元素,二维数组result存放子集组合。(也可以放到递归函数参数里)
递归函数参数需要startIndex,因为求子集也是组合,组合是无序,取过的元素不会重复取,for就要从startIndex开始,而不是从0开始。
2.递归终止条件
如上图剩余集合为空的时候,就是叶子节点。也就是startIndex已经大于数组的长度了,就终止了,因为没有元素可取了
其实可以不需要加终止条件,因为startIndex >= nums.size(),本层for循环本来也结束了。
3.单层搜索逻辑
求取子集问题,不需要任何剪枝!因为子集就是要遍历整棵树。
class Solution { List result = new ArrayList();// 存放符合条件结果的集合 LinkedList path = new LinkedList();// 用来存放符合条件结果 public List subsets(int[] nums) { subsetsHelper(nums, 0); return result; } private void subsetsHelper(int[] nums, int startIndex){ result.add(new ArrayList(path));//把所有节点都记录下来,就是要求的子集集合 if (startIndex >= nums.length){ //终止条件也可以不加 return; } for (int i = startIndex; i时间复杂度:O(n * 2^n));(循环n个元素,2^n表示所有可能的子集数量)
空间复杂度:O(n);(递归栈的深度最多为 n)
Leetcode 90.子集II
题目链接:90.子集II
大佬视频讲解:子集II视频讲解
个人思路
这道题和上面子集的区别就是,这道题里的集合里有重复元素了,而且求取的子集要去重,这就用到了之前组合问题中的同一层去重(树层去重), 去重要用到标记数组used
解法
回溯法
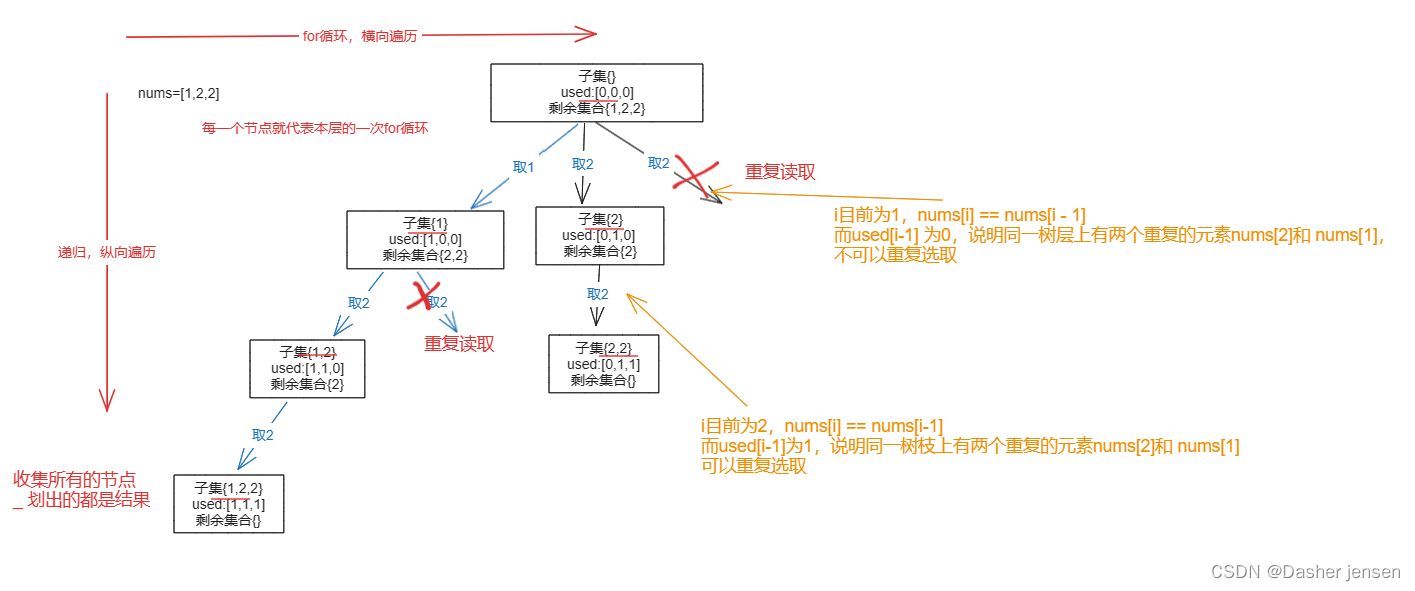
把子集问题抽象为如下树形结构
从图中可以看出,同一树层上重复取2 就要过滤掉,同一树枝上就可以重复取2,因为同一树枝上元素的集合才是唯一子集!
这道题的逻辑和 Leetcode 40.组合总和II 一样,搞清楚同一树层去重就能解决这道题。
class Solution { List result = new ArrayList();// 存放符合条件结果的集合 LinkedList path = new LinkedList();// 用来存放符合条件结果 boolean[] used;//记录元素是否使用过,用来树层去重 public List subsetsWithDup(int[] nums) { if (nums.length == 0){ result.add(path); return result; } Arrays.sort(nums); used = new boolean[nums.length];//初始化一个全是false(0)的布尔数组 subsetsWithDupHelper(nums, 0); return result; } private void subsetsWithDupHelper(int[] nums, int startIndex){ result.add(new ArrayList(path)); if (startIndex >= nums.length){ return; } for (int i = startIndex; i 0 && nums[i] == nums[i - 1] && !used[i - 1]){//树层重复 continue; } path.add(nums[i]); used[i] = true; subsetsWithDupHelper(nums, i + 1); path.removeLast();//回溯 used[i] = false;//回溯 } } }时间复杂度:O(n * 2^n));(循环n个元素,2^n表示所有可能的子集数量)
空间复杂度:O(n);(递归栈的深度最多为 n)
以上是个人的思考反思与总结,若只想根据系列题刷,参考卡哥的网址代码随想录算法官网