【编译原理】实验一——正则运算表达式的 DFA 构建

一、基本数据结构

1）字符集

public class CharSet {
  /*
    字符进行范围运算('a'~'z')、并运算(a|b)和差运算(-) 都返回一个新的字符集对象
    */
  /** 字符集id */
  private final int indexId;
  /** 字符集中的段 id。一个字符集可以包含多个段 */
  private final int segmentId;
  /** 段的起始字符 */
  private final char fromChar;
  /** 段的结尾字符 */
  private final char toChar;
}

2）字符集表定义

/**
 * 字符集表的定义
 */
static public ArrayList pCharSetTable = new ArrayList();

3）NFA或DFA定义

public class Graph {
  static private int graphIdNum = 0;
  private int graphId;
  private int numOfStates;
  private State start;
  private ArrayList pEndStateTable;
  private ArrayList pEdgeTable;
  private ArrayList pStateTable;
}

4）边定义

public class Edge {
  private int fromState;
  private int nextState;
  private int driverId;
  private DriverType type;
}

5）状态定义

public class State {
  private int stateId;
  private StateType type;
  private LexemeCategory category;
  static private int stateIdNum = 0;
}

6）转换枚举类型

public enum DriverType {
  // 空字符
  NULL,
  // 字符
  CHAR,
  // 字符集
  CHARSET
}

7）词类别枚举类型

public enum LexemeCategory {
  // 空字符
  EMPTY,
  // 整数常量
  INTEGER_CONST,
  // 实数常量
  FLOAT_CONST,
  // 科学计数法常量
  SCIENTIFIC_CONST,
  // 数值运算词
  NUMERIC_OPERATOR,
  // 注释
  NOTE,
  // 字符串常量
  STRING_CONST,
  // 空格常量
  SPACE_CONST,
  // 比较运算词
  COMPARE_CONST,
  // 变量词
  ID,
  // 逻辑运算词
  LOGIC_OPERATOR,
  // 关键字
  KEYWORD
}

8）状态取值枚举类型

public enum StateType {
  // 匹配和不匹配
  MATCH,
  UNMATCH
}

9）正则表达式定义

public class RegularExpression {
  int regularId;
  String name;
  /**
   * 正则运算符，共有 7 种：‘=’, ‘~’，‘-’, ‘|’，‘.’, ‘*’, ‘+’, ‘?’
   */
  char operatorSymbol;
  /**
   * 左操作数
    */
  int operandId1;
  /**
   * 右操作数（一元运算时为null）
   */
  int operandId2;
  /**
   * 左操作数的类型
   */
  OperandType type1;
  /**
   * 右操作数的类型（一元运算时为null）
   */
  OperandType type2;
  /**
   * 运算结果的类型
   */
  OperandType resultType;
  /**
   * 词的 category 属性值
   */
  LexemeCategory category;
  /**
   * 对应的 NFA
   */
  Graph pNFA;
}

二、针对字符集的创建，实现如下函数

1）int range (char fromChar, char toChar)； // 字符的范围运算

函数作用：得到起始字符到结束字符之间的任意字符集

实现方法：新建一个字符集，直接加入字符集表即可。

实现函数：

public static int range(char fromChar, char toChar) {
  /**
   * 字符的范围运算
   */
  CharSet c = new CharSet(fromChar, toChar);
  pCharSetTable.add(c);
  return c.getIndexId();
}

2）int union(char c1, char c2)； // 字符的并运算

函数作用：进行字符与字符之间的并运算

实现方法：新建一个字符集对象，判断c1和c2是否相等，不相等的话新建一个段，加入字符集表

实现函数：

public static int union(char c1, char c2) {
  /**
   * 字符的并运算
   */
  CharSet charSet1 = new CharSet(c1, c1);
  pCharSetTable.add(charSet1);
  if (c1 != c2) {
    CharSet charSet2 = new CharSet(c1, c2, charSet1.getIndexId());
    pCharSetTable.add(charSet2);
  }
  return charSet1.getIndexId();
}

3）int union(int charSetId, char c)；// 字符集与字符之间的并运算

函数作用：进行字符和字符集之间的并运算

实现方法：先新建一个字符集，获取其stateId，把原字符集的所有段赋值给新建字符集，再给字符新建一个段，放入字符集表中。最后返回新得到的字符集的Id。

实现函数：

public static int union(int CharSetId, char c) {
  /**
   * 字符集与字符之间的并运算
   */
  int newId = 0;
  boolean flag = false;
  for (CharSet charSet: pCharSetTable) {
    if (charSet.getIndexId() == CharSetId) {
      if (flag) {
        // 新建一个段
        CharSet newCharSet = new CharSet(charSet.getFromChar(), charSet.getToChar(), newId);
        pCharSetTable.add(newCharSet);
      }
      else {
        // 新建一个字符集
        CharSet newCharSet = new CharSet(charSet.getFromChar(), charSet.getToChar());
        newId = newCharSet.getIndexId();
        pCharSetTable.add(newCharSet);
        flag = true;
      }
    }
  }
  CharSet newSegment = new CharSet(c, c, newId);
  pCharSetTable.add(newSegment);
  return newId;
}

4）int union(int charSetId1,int charSetId2)；//字符集与字符集的并运算

函数作用：字符集与字符集的并运算

实现方法：直接将两个字符集的所有段加到新的字符集中，并返回相应Id即可。

实现函数：

public static int union(int CharSetId1, int CharSetId2) {
  /**
   * 字符集与字符集的并运算
   */
  int newId = 0;
  boolean flag = false;
  ArrayList addList = new ArrayList();
  for (CharSet charSet: pCharSetTable) {
    if (charSet.getIndexId() == CharSetId1) {
      if (flag) {
        // 新建一个段
        CharSet newCharSet = new CharSet(charSet.getFromChar(), charSet.getToChar(), newId);
        addList.add(newCharSet);
      }
      else {
        // 新建一个字符集
        CharSet newCharSet = new CharSet(charSet.getFromChar(), charSet.getToChar());
        newId = newCharSet.getIndexId();
        addList.add(newCharSet);
        flag = true;
      }
    }
  }
  for (CharSet charSet: pCharSetTable) {
    if (charSet.getIndexId() == CharSetId2) {
      // 新建一个段
      CharSet newCharSet = new CharSet(charSet.getFromChar(), charSet.getToChar(), newId);
      addList.add(newCharSet);
    }
  }
  for (CharSet charSet: addList) {
    pCharSetTable.add(charSet);
  }
  return newId;
}

5）int difference(int charSetId, char c)； // 字符集与字符之间的差运算

实现方法：判断字符是否在字符集中间，如果不在就将原字符集的所有段赋值给新的字符集，如果在的话就分为两个段，但是在边界条件上只需新建一个段。最后返回新字符集id即可。

实现函数：

public static int difference(int CharSetId, char c) {
  /**
   * 字符集与字符之间的差运算
   */
  int newId = 0;
  boolean flag = false;
  for (CharSet charSet: pCharSetTable) {
    if (charSet.getIndexId() == CharSetId) {
      if (charSet.getFromChar()  c) {
        if (flag) {
          // 新建一个段
          CharSet newCharSet1 = new CharSet(charSet.getFromChar(), (char)(c-1), newId);
          pCharSetTable.add(newCharSet1);
        }
        else {
          // 新建一个字符集
          CharSet newCharSet1 = new CharSet(charSet.getFromChar(), (char)(c-1));
          newId = newCharSet1.getIndexId();
          pCharSetTable.add(newCharSet1);
          flag = true;
        }
        CharSet newCharSet2 = new CharSet((char)(c+1), charSet.getToChar(), newId);
        pCharSetTable.add(newCharSet2);
      }
      else if (charSet.getFromChar() == c) {
        if (flag) {
          // 新建一个段
          CharSet newCharSet = new CharSet((char)(c+1), charSet.getToChar(), newId);
          pCharSetTable.add(newCharSet);
        }
        else {
          // 新建一个字符集
          CharSet newCharSet = new CharSet((char)(c+1), charSet.getToChar());
          newId = newCharSet.getIndexId();
          pCharSetTable.add(newCharSet);
          flag = true;
        }
      }
      else if (charSet.getToChar() == c) {
        if (flag) {
          // 新建一个段
          CharSet newCharSet = new CharSet(charSet.getFromChar(), (char)(c-1), newId);
          pCharSetTable.add(newCharSet);
        }
        else {
          // 新建一个字符集
          CharSet newCharSet = new CharSet(charSet.getFromChar(), (char)(c-1));
          newId = newCharSet.getIndexId();
          pCharSetTable.add(newCharSet);
          flag = true;
        }
      }
      else {
        if (flag) {
          // 新建一个段
          CharSet newCharSet = new CharSet(charSet.getFromChar(), charSet.getToChar(), newId);
          pCharSetTable.add(newCharSet);
        }
        else {
          // 新建一个字符集
          CharSet newCharSet = new CharSet(charSet.getFromChar(), charSet.getToChar());
          newId = newCharSet.getIndexId();
          pCharSetTable.add(newCharSet);
          flag = true;
        }
      }
    }
  }
  return newId;
}

三、基于NFA的数据结构定义，按照最简NFA构造法，实现如下函数。

1）Graph * generateBasicNFA(DriverType driverType，int driverId );

函数作用：构造一个最简单的NFA

实现方法：构造两个状态，一个初状态，一个末状态。此处新增了一个category属性便于之后词法分析的识别。

实现函数：

public static Graph generateBasicNFA(DriverType driverType, int driverId, LexemeCategory category) {
  Graph pNFA= new Graph();
  State pState1 = new State(0, StateType.UNMATCH, LexemeCategory.EMPTY);
  State pState2 = new State(1, StateType.MATCH, category);
  Edge edge = new Edge(pState1.getStateId(), pState2.getStateId(), driverId, driverType);
  // 加入NFA中
  pNFA.addState(pState1);
  pNFA.setStart(pState1);
  pNFA.addState(pState2);
  pNFA.addEdge(edge);
  return pNFA;
}

2）Graph * union(Graph * pNFA1, Graph * pNFA2)； // 并运算

函数作用：两个NFA进行并运算。

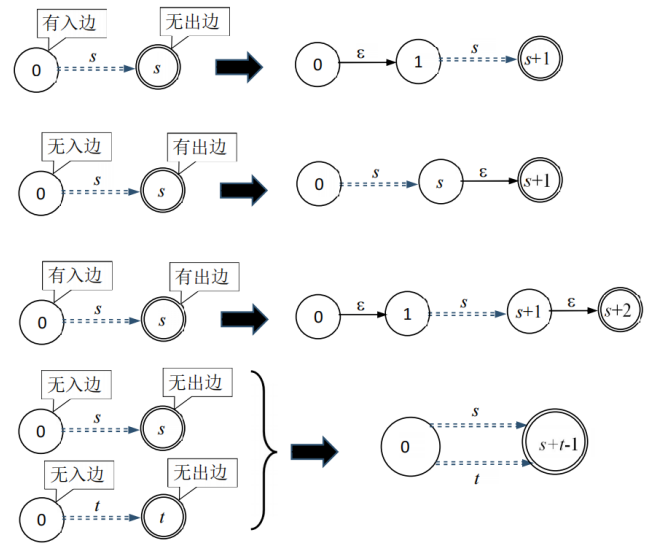
实现方法：新建一个图和初始状态，对原来的两个NFA进行等价改造，再合并其初始状态和终结状态即可。等价改造规则如下：

实现函数：

public static Graph union(Graph pNFA1, Graph pNFA2) {
  /**
   * 并运算
   */
  Graph graph = new Graph();
  // 并运算之前对pNFA1和pNFA2进行等价改造
  pNFA1.change();
  pNFA2.change();
  // 获取初始状态
  State start = pNFA1.getStart();
  graph.setStart(start);
  // 获取状态数目
  int stateNum1 = pNFA1.getNumOfStates();
  int stateNum2 = pNFA2.getNumOfStates();
  graph.setNumOfStates(stateNum1+stateNum2-2);
  // 重新编号并加入新的graph
  pNFA2.reNumber(stateNum1-2);
  // 将pNFA1和pNFA2加入结果图中
  graph.addTable(pNFA1);
  graph.addTable(pNFA2);
  // 合并终结状态
  graph.mergeEnd(pNFA1, stateNum1+stateNum2-3);
  // 合并初始状态
  graph.mergeStart(pNFA2);
  return graph;
}

其中具体函数实现如下：

1.change函数：若初始状态存在入边，则新增一个初始状态，用ε边连接原初始状态；若终结状态存在出边，则构造一个状态设为终结状态，所有原终结状态连接该状态。

public int change() {
  /**
   * 对NFA进行等价改造
   */
  int changeType = 0;
  // 初始状态有入边
  if (haveInSide(start)) {
    // 新增一个状态
    State newStart = new State(0, StateType.UNMATCH, LexemeCategory.EMPTY);
    addState(newStart);
    // 重新编号
    reNumber(1);
    // 添加一条newStart到初始状态的ε边
    Edge edge = new Edge(0, 1, DriverType.NULL);
    pEdgeTable.add(edge);
    // 设置初始状态
    start = newStart;
    // 最低位为1表示初始状态有入边
    changeType |= 1;
  }
  if (haveOutside(pEndStateTable)) {
    // 新增一个状态
    State newEnd = new State(pStateTable.size(), StateType.UNMATCH, LexemeCategory.EMPTY);
    addState(newEnd);
    // 添加结束状态到newEnd的ε边
    for (State state: pEndStateTable) {
      Edge edge = new Edge(state.getStateId(), newEnd.getStateId(), DriverType.NULL);
      pEdgeTable.add(edge);
    }
    // 清空当前结束状态
    pEdgeTable.clear();
    // 设置新的结束状态
    pEndStateTable.add(newEnd);
    // 第二低位为1表示终结状态有出边
    changeType |= 2;
  }
  return changeType;
}

haveInSide函数：判断是否有边到达初始状态

public boolean haveInSide(State start) {
  /**
   * 判断是否有边到达初始状态
   */
  for (Edge edge : pEdgeTable) {
    if (edge.getNextState() == start.getStateId()) {
      return true;
    }
  }
  return false;
}

haveOutSide函数：判断是否有边从终结状态出发

public boolean haveOutside(ArrayList stateArrayList) {
  /**
   * 判断是否有边从结束状态出发
   */
  for (Edge edge : pEdgeTable) {
    for (State state : stateArrayList) {
      if (edge.getFromState() == state.getStateId()) {
        return true;
      }
    }
  }
  return false;
}

2.reNumber函数：对状态和边对应的状态重新编号，确保状态有序。

public void reNumber(int index) {
  // 状态重新编号
  for (State state : pStateTable) {
    int stateId = state.getStateId();
    state.setStateId(stateId+ index);
  }
  // 边重新编号
  for (Edge edge : pEdgeTable) {
    int fromState = edge.getFromState();
    edge.setFromState(fromState + index);
    int nextState = edge.getNextState();
    edge.setNextState(nextState + index);
  }
}

3.addTable函数：将参数NFA中的所有边、状态、结束状态（均已重新编号）加入到该NFA中。

public void addTable(Graph g) {
  pEdgeTable.addAll(g.getpEdgeTable());
  pStateTable.addAll(g.getpStateTable());
  pEndStateTable.addAll(g.pEndStateTable);
}

4.mergeEnd函数：将pNFA1的终结状态合并到pNFA2中，终结状态的序号为最大值，即stateNum1+stateNum2-3

public void mergeEnd(Graph NFA, int endStateId) {
  ArrayList endRemoveList = new ArrayList();
  for (State state: NFA.pEndStateTable) {
    for (Edge edge: NFA.getpEdgeTable()) {
      // 找到所有到达终结状态的边
      if (edge.getNextState() == state.getStateId()) {
        edge.setNextState(endStateId);
      }
    }
    pStateTable.remove(state);
    endRemoveList.add(state);
  }
  for (State state: endRemoveList) {
    pEndStateTable.remove(state);
  }
}

5.mergeStart函数：将pNFA2的初始状态合并到pNFA1中，初始状态的序号为0

public void mergeStart(Graph NFA) {
  State start = NFA.getStart();
  for (Edge edge: NFA.getpEdgeTable()) {
    // 找到所有从初始状态出发的边
    if (edge.getFromState() == start.getStateId()) {
      edge.setFromState(0);
    }
  }
  pStateTable.remove(start);
}

3）Graph * product(Graph * pNFA1, Graph * pNFA2); // 连接运算

函数作用：对两个NFA进行连接运算

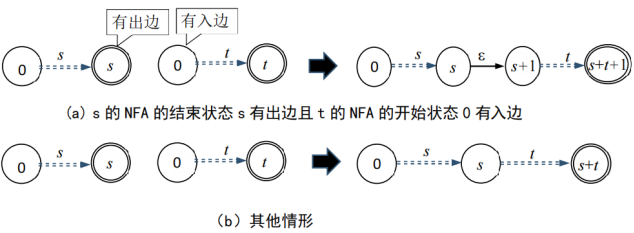
实现思路：NFA的连接运算分为两种情况，情况之一是前一个图的接收状态有出边，后一个图的初状态有入边，则需要中间添加一个状态来防止倒灌；其余的情况则是前一个的接收状态和后一个的初状态合二为一，然后根据状态Id的变化添加Id和添加边即可。最后返回一个新建的图。

实现函数：

public static Graph product(Graph pNFA1, Graph pNFA2) {
  /**
   * 连接运算
   */
  Graph graph = new Graph();
  // 获取初始状态，编号为0
  State start = pNFA1.getStart();
  graph.setStart(start);
  // 添加pNFA1到结果中
  graph.addTable(pNFA1);
  // 获取状态数目
  int stateNum1 = pNFA1.getNumOfStates();
  int stateNum2 = pNFA2.getNumOfStates();
  // 判断有无出入边
  if (pNFA1.haveOutside(pNFA1.getpEndStateTable()) && pNFA2.haveInSide(pNFA2.getStart())) {
    // 重新编号
    pNFA2.reNumber(stateNum1);
    // 设置状态信息
    graph.setNumOfStates(stateNum1+stateNum2);
    // 添加ε边
    for (State state:pNFA1.getpEndStateTable()) {
      Edge edge = new Edge(state.getStateId(), pNFA2.getStart().getStateId(), DriverType.NULL);
      graph.addEdge(edge);
    }
  }
  else {
    // 重新编号
    pNFA2.reNumber(stateNum1-1);
    // 初始状态和pNFA2的终结状态合并
    pNFA2.removeStateById(stateNum1-1);
    // 设置状态信息
    graph.setNumOfStates(stateNum1+stateNum2-1);
  }
  for (State state: graph.getpStateTable()) {
    state.setType(StateType.UNMATCH);
  }
  graph.setpEndStateTable(new ArrayList());
  // 构建pNFA1到pNFA2的边
  graph.addTable(pNFA2);
  return graph;
}

4）Graph * plusClosure(Graph * pNFA) //正闭包运算

函数作用：实现除了0个以外的图重复

实现思路：因为没有0到结束状态的干扰，可以直接添加一条边，从接收状态到初状态，转换条件为空。

实现函数：

public static Graph plusClosure(Graph pNFA) {
  /**
   * 正闭包运算
   */
  Graph graph = new Graph();
  // 构建初始状态，即pNFA的初始状态
  State start = pNFA.getStart();
  graph.setStart(start);
  // 获取状态数目
  int stateNum1 = pNFA.getNumOfStates();
  graph.setNumOfStates(stateNum1);
  // 构建pNFA从结束到开始的边
  graph.addTable(pNFA);
  pNFA.addEndEdgeToOther(pNFA.getStart());
  return graph;
}

5）Graph * closure(Graph * pNFA) // 闭包运算

函数作用：包含0次和很多次的图的重复

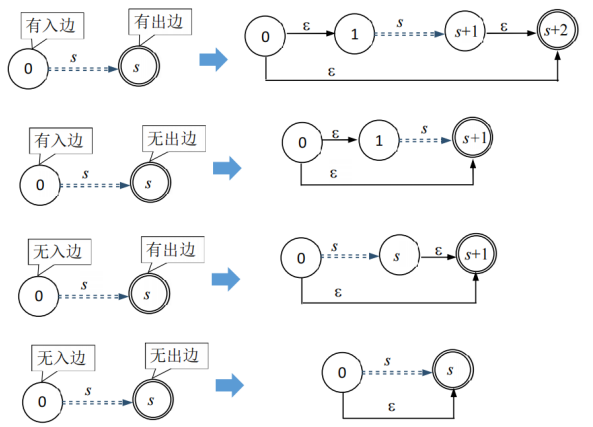
实现思路：在4的基础上增加一个从初始状态到接收状态的边，此处此时需要考虑初状态是否有入边，接受状态是否有出边，即首先进行规范化。最后返回新建的图。

实现函数：

public static Graph closure(Graph pNFA) {
  /**
   * 闭包运算
   */
  State start = pNFA.getStart();
  ArrayList endStateList = pNFA.getpEndStateTable();
  // 判断出入边，并添加相关状态信息
  int changeType = pNFA.change();
  if (changeType == 0) {
    // 无出入边，终结状态合并到开始状态
    pNFA.mergeEnd(pNFA, 0);
    pNFA.setNumOfStates(pNFA.getpStateTable().size());
    for (State state: pNFA.getpStateTable()) {
      if (state.getStateId() == 0) {
        state.setType(StateType.MATCH);
        pNFA.addEndState(state);
      }
    }
  }
  else {
    // 添加从原开始状态到原终结状态的ε边
    for (State state: endStateList) {
      Edge edge = new Edge(state.getStateId(), start.getStateId(), DriverType.NULL);
      pNFA.addEdge(edge);
    }
    // 添加从开始到终结的ε边
    start = pNFA.getStart();
    ArrayList edgeList = new ArrayList();
    for (State state: pNFA.getpEndStateTable()) {
      Edge edge = new Edge(start.getStateId(), state.getStateId(), DriverType.NULL);
      // 由于涉及到更改结束状态集合的操作，因此需要先遍历再添加边
      edgeList.add(edge);
    }
    for (Edge edge: edgeList) {
      pNFA.addEdge(edge);
    }
  }
  // 新建一个NFA，复制进来即可
  Graph graph = new Graph(pNFA);
  return graph;
}

6）Graph * zeroOrOne(Graph * pNFA)； // 0 或者 1 个运算。

函数作用：进行图的一次或者0次运算

实现思路：在实现之前先进行规范化，、再添加一条初状态到接受状态的边。

实现函数：

public static Graph zeroOrOne(Graph pNFA) {
  /**
   * 0 或者 1 个运算。
   */
  Graph graph = new Graph();
  // 获取初始状态
  State start = pNFA.getStart();
  graph.setStart(start);
  graph.addTable(pNFA);
  // 根据出入边添加或调整状态信息
  graph.change();
  // 设置状态数目
  graph.setNumOfStates(graph.getpStateTable().size());
  // 构建pNFA的初始状态到终结状态的边
  for (State state: graph.getpEndStateTable()) {
    Edge edge = new Edge(start.getStateId(), state.getStateId(), DriverType.NULL);
    graph.addEdge(edge);
  }
  return graph;
}

三、基于NFA数据结构定义，实现如下函数。

1）子集构造法

list move(Graph * pNFA, list stateIdTable, int driverId)

函数作用：找到从一个状态集合通过某个转换条件可以跳转到的下一个状态集合

实现思路：循环该表的边集合，如果出现开始状态是存在对应集合中，并且是该引导条件Id，则将该状态id存入set（因为set可以消除重复元素）中，再将状态集合从set中放到list中并返回。

实现函数：

public static ArrayList move(Graph graph, int stateId, int driveId) {
  /**
   * 状态转移函数
   */
  ArrayList edgeArrayList = graph.getpEdgeTable();
  ArrayList stateArrayListAnswer = new ArrayList();
  for (Edge edge: edgeArrayList) {
    if (edge.getFromState() == stateId && edge.getDriverId() == driveId) {
      int nextState = edge.getNextState();
      stateArrayListAnswer.add(nextState);
    }
  }
  return stateArrayListAnswer;
}

list ε_closure(Graph * pNFA, list stateIdTable)

函数作用：得到状态集合中的所有空转换的状态集合

实现思路：将传入参数中的状态集合在此图上能够通过空转移转换到的状态都存到set中，最后再将状态Id从set中转移到list中并进行返回。因为可能会出现连续的多个空转移，故可在外面进行使用的时候对该函数进行循环，直到找全其空转换状态集合为止。

实现函数：

public static ArrayList closure(Graph graph, ArrayList stateArrayList) {
  /**
   * 求空闭包
   */
  ArrayList edgeArrayList = graph.getpEdgeTable();
  ArrayList resultStateArrayList, currentStateArrayList, nextSateArrayList = new ArrayList();
  resultStateArrayList = stateArrayList;
  currentStateArrayList = stateArrayList;
  while(!currentStateArrayList.isEmpty()) {
    // 找到能够空转换的状态集合
    for (Edge edge: edgeArrayList) {
      if (currentStateArrayList.contains(edge.getFromState()) && edge.getType() == DriverType.NULL) {
        if (!nextSateArrayList.contains(edge.getNextState())) {
          nextSateArrayList.add(edge.getNextState());
        }
      }
    }
    // 去除结果状态集合后的状态集合
    for (Integer stateId: resultStateArrayList) {
      if (nextSateArrayList.contains(stateId)) {
        nextSateArrayList.remove(stateId);
      }
    }
    // 去除后为空表示闭包搜索完毕
    if (nextSateArrayList.isEmpty()) {
      break;
    }
    else {
      resultStateArrayList.addAll(nextSateArrayList);
      currentStateArrayList = nextSateArrayList;
    }
  }
  return resultStateArrayList;
}

list DTran(Graph * pNFA, list stateIdTable,int driverId)

函数作用：将前面两个函数功能集合

实现思路：直接调用前面实现的函数并且对空转换进行多次循环

实现函数：

public static ArrayList dTran(Graph graph, ArrayList currentStateArrayList, int driveId) {
  /**
   * 状态转移集合
   */
  ArrayList nextStateArrayList = new ArrayList();
  for (int stateId: currentStateArrayList) {
    nextStateArrayList.addAll(move(graph, stateId, driveId));
  }
  return closure(graph, nextStateArrayList);
}

2）Graph * NFA_to_DFA(Graph *pNFA)

函数作用：将NFA转换为DFA

实现思路：保存整个图的驱动id，并且计算出初状态的空转换状态集合，然后通过此状态集合，对驱动id进行循环，调用DTran函数，得到可达的状态集合，并将这些状态集合都存入set中。接着从set中读取这些状态集合并且为其标号，向新建的DFA添加这些状态。接着通过这些状态再次对驱动id进行循环并且得到相应的状态集合，找到这些状态集合的对应的状态id，最后则得到了边，并将向DFA中添加这些边，最后返回DFA。

实现函数：

public static Graph NFAToDFA(Graph pNFA) {
  /**
   * NFA转换为DFA
   */
  Graph graph = new Graph();
  ArrayList edgeArrayList = pNFA.getpEdgeTable();
  // 初始状态的闭包
  State start = pNFA.getStart();
  ArrayList currentStateArrayList = new ArrayList();
  currentStateArrayList.add(start.getStateId());
  currentStateArrayList = closure(pNFA, currentStateArrayList);
  // 用于存储所有状态集合的集合
  ArrayList allStateList = new ArrayList();
  // 存储最终状态集合
  ArrayList edgeList = new ArrayList();
  // 存储开始状态
  allStateList.add(currentStateArrayList);
  State startList = new State(0, StateType.UNMATCH, LexemeCategory.EMPTY);
  ArrayList stateList = new ArrayList();
  stateList.add(startList);
  graph.setStart(startList);
  // 存储结束状态集合
  ArrayList endStateList = new ArrayList();
  // 表示当前状态序号
  int currentState = 0;
  while (currentState  
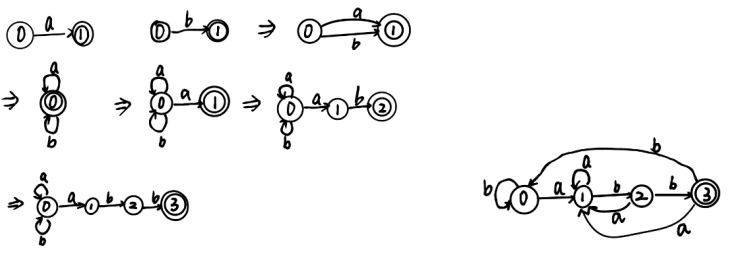
四、请以正则表达式(a|b)*abb 来测试，检查实现代码的正确性
实现思路：依次构建正则表达式的NFA图，再将其转换为DFA图
实现代码：
 
public void test() {
  /**
   * 测试(a|b)*abb
   */
  // 构建字符集表
  int driveIda = Problem1.range('a', 'a');
  int driveIdb = Problem1.range('b', 'b');
  System.out.println(driveIda);
  System.out.println(driveIdb);
  // 构建NFA图
  // a
  Graph graphA = Problem2.generateBasicNFA(DriverType.CHAR, driveIda, LexemeCategory.EMPTY);
  System.out.println("a");
  System.out.println(graphA);
  // b
  Graph graphB = Problem2.generateBasicNFA(DriverType.CHAR, driveIdb, LexemeCategory.EMPTY);
  System.out.println("b");
  System.out.println(graphB);
  // a|b
  Graph graphAUnionB = Problem2.union(graphA, graphB);
  System.out.println("a|b");
  System.out.println(graphAUnionB);
  // (a|b)*
  Graph graphClosure = Problem2.closure(graphAUnionB);
  System.out.println("(a|b)*");
  System.out.println(graphClosure);
  // (a|b)*a
  graphA = Problem2.generateBasicNFA(DriverType.CHAR, driveIda, LexemeCategory.EMPTY);
  System.out.println("(a|b)*a");
  Graph graphAndA = Problem2.product(graphClosure, graphA);
  System.out.println(graphAndA);
  // (a|b)*ab
  graphB = Problem2.generateBasicNFA(DriverType.CHAR, driveIdb, LexemeCategory.EMPTY);
  Graph graphAndB = Problem2.product(graphAndA, graphB);
  System.out.println("(a|b)*ab");
  System.out.println(graphAndB);
  // (a|b)*abb
  graphB = Problem2.generateBasicNFA(DriverType.CHAR, driveIdb, LexemeCategory.EMPTY);
  Graph graphEnd = Problem2.product(graphAndB, graphB);
  System.out.println("(a|b)*abb");
  System.out.println(graphEnd);
  // NFA转化为DFA
  Graph graphDFA = Problem3.NFAToDFA(graphEnd);
  System.out.println(graphDFA);
}
 
生成结果:
 
代码输出如下：
 

正则表达式	输出	NFA图
a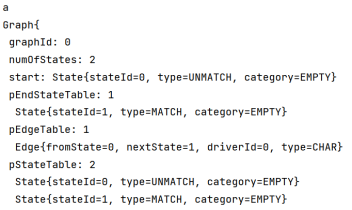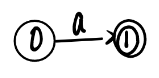
b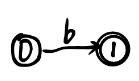
a|b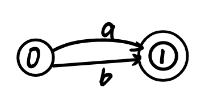
(a|b)*
(a|b)*a
(a|b)*ab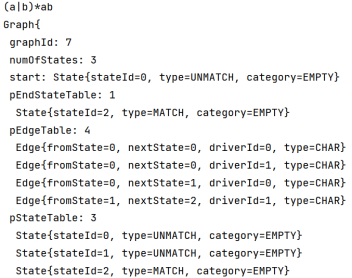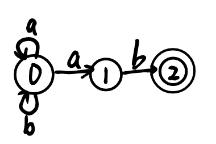
(a|b)*abb
(a|b)*abb

以 TINY 语言的词法来验证程序代码的正确性。

1.构建字符集表

// 构建字符集表
int charSetLetterLower = Problem1.range('a', 'z');
int charSetLetterUpper = Problem1.range('A', 'Z');
int charSetDigit = Problem1.range('0', '9');
int charSetLetter = Problem1.union(charSetLetterLower, charSetLetterUpper);
ArrayList charSetLetterList = new ArrayList();
for (char c = 'a'; c 
  charSetLetterList.add(Problem1.range(c, c));
}
int charSetAdd = Problem1.range('+', '+');
int charSetSub = Problem1.range('-', '-');
int charSetMul = Problem1.range('*', '*');
int charSetDiv = Problem1.range('/', '/');
int charSetEqual = Problem1.range('=', '=');
int charSetSmall = Problem1.range('