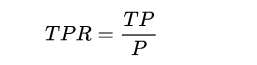ROC曲线及Python绘制方法

一、ROC曲线简介

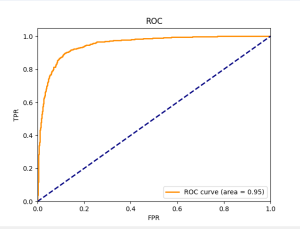
ROC的全名叫做Receiver Operating Characteristic，中文名“受试者工作特征曲线”，其主要分析工具是一个画在二维平面上的曲线——ROC 曲线。平面的横坐标是false positive rate(FPR)，纵坐标是true positive rate(TPR)。对某个分类器而言，我们可以根据其在测试样本上的表现得到一个TPR和FPR点对。这样，此分类器就可以映射成ROC平面上的一个点。调整这个分类器分类时候使用的阈值，我们就可以得到一个经过(0, 0)，(1, 1)的曲线，这就是此分类器的ROC曲线。 一般情况下，这个曲线都应该处于(0, 0)和(1, 1)连线的上方。因为(0, 0)和(1, 1)连线形成的ROC曲线实际上代表的是一个随机分类器。如果很不幸，你得到一个位于此直线下方的分类器的话，一个直观的补救办法就是把所有的预测结果反向，即：分类器输出结果为正类，则最终分类的结果为负类，反之，则为正类。虽然，用ROC 曲线来表示分类器的性能很直观好用。可是，人们总是希望能有一个数值来标志分类器的好坏。于是Area Under roc Curve(AUC)就出现了。顾名思义，AUC的值就是处于ROC 曲线下方的那部分面积的大小。通常，AUC的值介于0.5到1.0之间，较大的AUC代表了较好的性能。AUC（Area Under roc Curve）是一种用来度量分类模型好坏的一个标准。

二、基本概念

2.1 分类方式

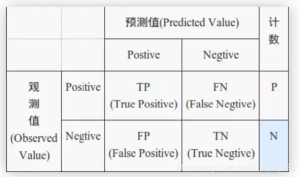
真正（True Positive , TP），模型预测为正的正样本；

假负（False Negative , FN），模型预测为负的正样本；

假正（False Positive , FP），模型预测为正的负样本；

真负（True Negative , TN），模型预测为负的负样本。

2.2 横纵坐标

横坐标：假阳性率（False Positive Rate, FPR），N是真实负样本的个数， FP是N个负样本中被分类器预测为正样本的个数。

纵坐标：真阳性率（True Positive Rate, TPR），P是真实正样本的个数， TP是P个正样本中被分类器预测为正样本的个数。

2.3 ROC优势

ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡（class imbalance）现象，即负样本比正样本多很多（或者相反），而且测试数据中的正负样本的分布也可能随着时间变化。

2.4 AUC

• AUC： ROC曲线下方的面积，取值范围一般在0.5和1之间。
• AUC值越大的分类器，正确率越高

  三、Python编程画ROC曲线

  3.1 实现方法

  • 绘制ROC曲线主要使用python 的sklearn库中的两个函数，roc_curv和auc两个函数。
  • roc_curv 用于计算出FPR假阳性率）和TPR（真阳性率）
  • auc用于计算曲线下面积，输入为FPR、TPR

    3.2 roc_curv函数

    roc_curve(y_true, y_score, pos_label=None, sample_weight=None,drop_intermediate=True)

    输入值

    y_true ：一个和样本数量一致的一维向量，数据是正确的二元标签。如果标签不是{- 1,1}或{0,1}，则可以显式指定pos_label。

    sample_weight：一个样本数量一致的一维向量，指定每个样本的权重，默认不输入。

    drop_intermediate：为true时(默认= True)会删除一些不会出现在ROC曲线上的次优阈值。

    y_score：一个样本数量一致的一维向量，目标分数可以是阳性类的概率估计、置信度值或决策的非阈值度量(在某些分类器上由“decision_function”返回，比如SVM)。就是对测试集进行分类后得到的一个用于衡量该类是阳性还是阴性的分数度量，分类器也是根据这个分数来判断测试集是阳性样本还是阴性样本，因此通常都可以在分类器的中间过程拿到这个分数。

    pos_label：样本标签，如果y_true不满足{0,1},{-1,1}标签时则需要通过该参数指定那些是阳性样本，其余的则为阴性样本，默认不输入。

    返回值

    FPR:假阳性率序列，数量与thread一致的一维向量。

    TPR:真阳性率序列，数量与thread一致的一维向量。

    thread:该序列是一个递减序列，在每一个阈值下对y_score进行划分，大于的视为阳性，小于的视为阴性，从而计算出该阈值下的FPR。

    3.3 Python代码

    import numpy as np
    from sklearn.model_selection import train_test_split
    from sklearn.datasets import make_classification
    from sklearn.linear_model import LogisticRegression
    from sklearn.metrics import roc_curve, auc
    import matplotlib.pyplot as plt
      
    # 生成更多的数据 
    #10000个样本和20个特征的分类问题
    X, y = make_classification(n_samples=10000, n_features=20, n_informative=2, n_redundant=10, random_state=42) 
     
    # 划分训练集和测试集  ,测试集占0.3
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)  
     
    # 使用逻辑回归作为分类器 ，random_state参数设置为42，用于确保每次运行代码时，都能获得相同的随机结果，从而可以复现结果。
    classifier = LogisticRegression(random_state=42)  
    classifier.fit(X_train, y_train)
     
    # 预测概率  ，给定测试数据，返回预测的每个类别的概率。
    y_score = classifier.predict_proba(X_test)[:, 1]  
      
    # 计算ROC曲线  
    fpr, tpr, _ = roc_curve(y_test, y_score)  
    roc_auc = auc(fpr, tpr)  
      
    # 绘制ROC曲线  
    plt.figure()  
    lw = 2  
    plt.plot(fpr, tpr, color='darkorange', lw=lw, label='ROC curve (area = %0.2f)' % roc_auc)  
    plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')  
    plt.xlim([0.0, 1.0])  
    plt.ylim([0.0, 1.05])  
    plt.xlabel('FPR')  
    plt.ylabel('TPR')  
    plt.title('ROC')  
    plt.legend(loc="lower right")  
    plt.show()

    3.4 实验结果