动态规划-背包问题 分析+代码

这里写自定义目录标题

• 介绍背包问题
• 过程分析
• 例题
• • 题目说明
  • 代码
  • 输出结果

    介绍背包问题

    • 背景：在现实生活中，我们常常会面临需要在有限空间内做出最优选择的情况，比如旅行时需要选择携带哪些物品，或者在资源有限的情况下选择最有利可图的投资项目。而背包问题就是这样一类经典的组合优化问题，在计算机科学和算法设计领域具有重要的研究价值和应用意义。

    • 描述：背包问题是指给定一个容量为W的背包和一组物品，每个物品有自己的重量和价值。需要从这组物品中选择一些放入背包中，使得放入背包的物品总价值最大化，同时不能超过背包的容量。这个问题可以分为两种常见形式：0-1背包问题和完全背包问题。

      过程分析

      解决背包问题的常见方法是使用动态规划。具体过程如下：

      • 定义状态：使用一个二维数组dp[i][j]表示前i个物品放入容量为j的背包中所能获得的最大价值。
      • 状态转移方程：根据题目要求，推导出状态转移方程，通常分为当前物品放入背包和不放入背包两种情况。
      • 边界条件：初始化边界条件，通常第0行和第0列为0。
      • 递推计算：根据状态转移方程，逐步填充dp数组。
      • 返回结果：最终dp数组右下角的值即为所求的最大总价值。

        例题

        题目说明

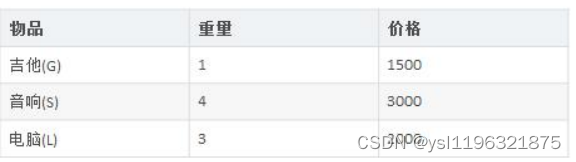
        • 背包问题:有一个背包，容量为4磅，现有如下物品

          

        • 1. 要求达到的目标为装入的背包的总价值最大，并且重量不超出
        • 1. 要求装入的物品不能重复
        • 1. 背包问题主要是指一个给定容量的背包、若干具有一定价值和重量的物品，如何选择物品放入背包使物品的价值最大。其中又分01 背包和完全背包

             (完全背包指的是:每种物品都有无限件可用)

        • 1. 这里的问题属于01背包，即每个物品最多放一个。而无限背包可以转化为01背包。
        • 1. 算法的主要思想，利用动态规划来解决。每次遍历到的第i个物品，根据w[i]和 v[i]来确定是否需要将该物品
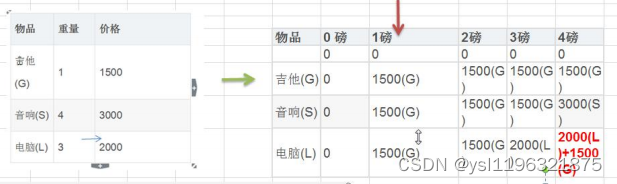
        • 放入背包中。即对于给定的n个物品,设v[i]、w[i]分别为第i个物品的价值和重量,C为背包的容量。再令v[i][j]

          表示在前i个物品中能够装入容量为j的背包中的最大价值。则我们有下面的结果:

          

        • 图片：

          -

          代码

          public class dongTaiGuiHua {
              public static void main(String[] args) {
                  int[] w = {1,4,3};
                  int[] val = {1500,3000,2000};
                  int m = 4 ; //背包容量
                  int n = val.length; //物品个数
                  //表示最大的价值
                  int[][] v = new int[ n+ 1][m + 1];
                  //初始化第一行
                  for (int i = 0; i = w[i - 1]){
                              v[i][j] =  Math.max( v[i - 1][j],val[i - 1] + v[i - 1][j - w[i - 1]]);
                          }
                      }
                  }
                  System.out.println(" --------------------");
                  //遍历展示
                  for (int i = 0; i  
          输出结果
           
          0 0 0 0 0 
          0 0 0 0 0 
          0 0 0 0 0 
          0 0 0 0 0 
           --------------------
          0 0 0 0 0 
          0 1500 1500 1500 1500 
          0 1500 1500 1500 3000 
          0 1500 1500 2000 3500