什么是softmax

目录

所有项目代码+UI界面

一：回归和分类的区别与联系：

在回归问题中，我们的目标是预测连续的输出值，例如预测房价或股票价格等。回归问题通常涉及到连续变量的预测，输出值是一个实数或者是一个连续的数值。而在分类问题中，我们的目标是预测离散的输出值，例如将一张图片分类为猫或狗等。分类问题通常涉及到对于不同类别的分类，输出值是一个离散的标签或者是概率分布。分类问题输出的是物体所属的类别，回归问题输出的是物体的值。

而softmax回归中，解决的是多分类问题。

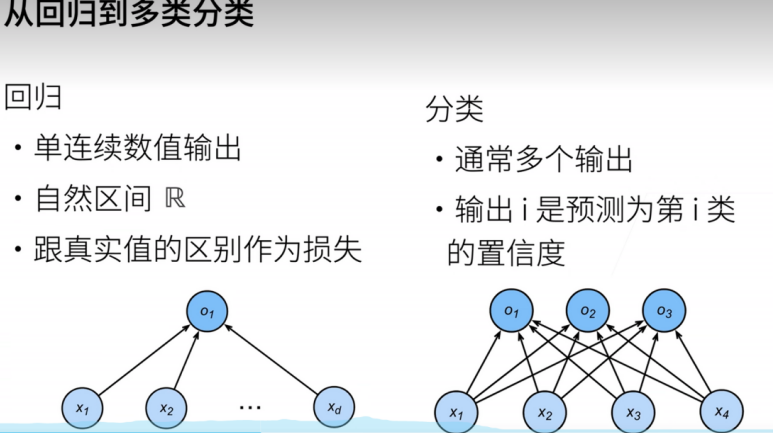
线性问题的优点在于它们具有良好的解析性质，例如闭式解和梯度下降等优化方法可以直接用于求解权重和偏置的最优值，但是它的建模能力有限，不能很好地捕捉复杂的非线性关系。

回归问题则通常指的是建模为一个多层神经网络的问题，这个神经网络可以拥有多个非线性激活函数，如sigmoid、tanh、ReLU等。通过堆叠多个非线性层，神经网络可以学习复杂的非线性关系，具有更强的建模能力。

回归可以用于预测多少的问题。 比如预测房屋被售出价格，或者棒球队可能获得的胜场数，又或者患者住院的天数。

事实上，我们也对分类问题感兴趣：不是问“多少”，而是问“哪一个”：

• 某个电子邮件是否属于垃圾邮件文件夹？

  • 某个用户可能注册或不注册订阅服务？

    • 某个图像描绘的是驴、狗、猫、还是鸡？

      • 某人接下来最有可能看哪部电影？

        我们从一个图像分类问题开始。 假设每次输入是一个2×2的灰度图像。 我们可以用一个标量表示每个像素值，每个图像对应四个特征x1,x2,x3,x4。 此外，假设每个图像属于类别“猫”“鸡”和“狗”中的一个。

        接下来，我们要选择如何表示标签。 我们有两个明显的选择：最直接的想法是选择y∈{1,2,3}， 其中整数分别代表狗猫鸡{狗,猫,鸡}。 这是在计算机上存储此类信息的有效方法。

        有一种表示表示分类数据的简单方法：独热编码（one-hot encoding）。 独热编码是一个向量，它的分量和类别一样多。 类别对应的分量设置为1，其他所有分量设置为0。 在我们的例子中，标签y将是一个三维向量， 其中(1,0,0)对应于“猫”、(0,1,0)对应于“鸡”、(0,0,1)对应于“狗”。

        二：softmax网络架构

        为了估计所有可能类别的条件概率，我们需要一个有多个输出的模型，每个类别对应一个输出。 为了解决线性模型的分类问题，我们需要和输出一样多的仿射函数（affine function）。 每个输出对应于它自己的仿射函数。 在我们的例子中，由于我们有4个特征和3个可能的输出类别， 我们将需要12个标量来表示权重（带下标的w）， 3个标量来表示偏置（带下标的b）。下面我们为每个输入计算三个未规范化的预测（logit）：o1,o2,o3。

        softmax回归也是一个单层神经网络。 由于计算每个输出o1,o2,o3。取决于所有输入x1,x2,x3,x4， 所以softmax回归的输出层也是全连接层。

        

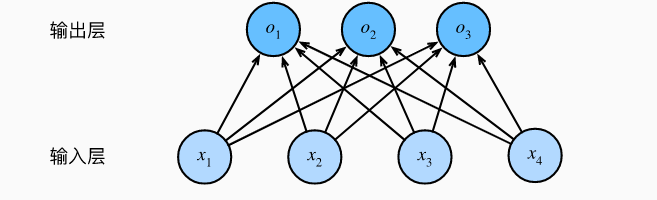
        为了更简洁地表达模型，我们仍然使用线性代数符号。 通过向量形式表达为o = Wx + b， 这是一种更适合数学和编写代码的形式。 由此，我们已经将所有权重放到一个3×4矩阵中。 对于给定数据样本的特征x， 我们的输出是由权重与输入特征进行矩阵-向量乘法再加上偏置b得到的。

        1.全连接层

        全连接层通常位于神经网络的中间层或者最后一层，它由多个神经元组成，每个神经元与前一层的所有神经元都有连接，即前一层的所有输出都会作为输入送到全连接层中的每个神经元。这些连接通常由可学习的权重和偏置参数来描述，其中权重参数用于控制输入信号的加权和，偏置参数用于对每个神经元的输出进行平移。全连接层的输出可以通过一个激活函数进行非线性映射，从而增加网络的非线性建模能力。

        2.前馈神经网络

        而前馈神经网络又是什么呢？它的名称来源于网络中信号的传递方向，即从输入层到输出层的单向传递，没有反馈连接。前馈神经网络通常由多个全连接层和激活函数组成，其中每个全连接层的输出作为下一层的输入。虽然前馈神经网络的结构比较简单，但是它可以学习到非常复杂的模式，具有强大的建模能力。

        3.反馈连接（Feedback Connection）

        是神经网络中一种特殊的连接方式，它允许网络中的信息从输出层反馈到输入层或中间层，从而影响网络的计算过程和学习过程。它可以使神经网络具有更强的记忆和适应能力，它可以使网络在处理时序数据、动态系统等任务中表现更加优秀。例如，在语音识别任务中，反馈连接可以帮助网络更好地利用上下文信息，提高识别准确率。在图像处理任务中，反馈连接可以使网络更好地处理时间序列信息，如视频分类、视频预测等。

        4.全连接层的参数量

        对于任何具有d个输入和p个输出的全连接层， 参数开销为O(np)，这个数字在实践中可能高得令人望而却步。 幸运的是，将d个输入转换为p个输出的成本可以减少到O(dq/n)， 其中超参数n可以由我们灵活指定，以在实际应用中平衡参数节约和模型有效性。

        5.softmax:对类别进行一位有效编码，不关心真实值，而更关心它的置信度，输出和为1

        我们希望模型的输出y^可以视为属于某一类的概率， 然后选择具有最大输出值的类别argmax(y^)作为我们的预测。 例如，如果y^1、y^2和y^3分别为0.1、0.8和0.1， 那么我们预测的类别是2这一类。

        然而我们能否将未规范化的预测（就好比线性模型的输出）直接视作我们感兴趣的输出呢？ 答案是否定的。 因为将线性层的输出直接视为概率时存在一些问题： 一方面，我们没有限制这些输出数字的总和为1。 另一方面，根据输入的不同，它们可以为负值，无法达到我们的需求。

        softmax函数能够将未规范化的预测变换为非负数并且总和为1，同时让模型保持 可导的性质。 为了完成这一目标，我们首先对每个未规范化的预测求幂，这样可以确保输出非负(使用e的指数)。 为了确保最终输出的概率值总和为1，我们再让每个求幂后的结果除以它们的总和。如下式：

        看公式可以发现，其实softmax本质是贝叶斯后验

        

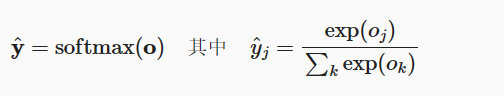
        这里，对于所有的j总有0≤y^≤1。 因此，y^可以视为一个正确的概率分布。 softmax运算不会改变未规范化的预测0之间的大小次序，只会确定分配给每个类别的概率。 因此，在预测过程中，我们仍然可以用下式来选择最有可能的类别。尽管softmax是一个非线性函数，但softmax回归的输出仍然由输入特征的仿射变换决定。 因此，softmax回归是一个线性模型。

        这里分享一个讲解线性转化为非线性的图解过程，对于我们入门小白非常友好：为什么神经网络可以学习几乎任何东西？_哔哩哔哩_bilibili

        小批量样本的矢量化

        这一部分对于刚接触softmax的来说不太好理解，最好用草稿纸推算一下，这样思路比较清晰。

        特征维度（输入数量）为d，批量大小为n。 此外，假设我们在输出中有q个类别。 那么小批量样本的特征为X∈R(n×d)， 权重为W∈R(d×q)， 偏置为b∈R(1×q)。 softmax回归的矢量计算表达式为：

        

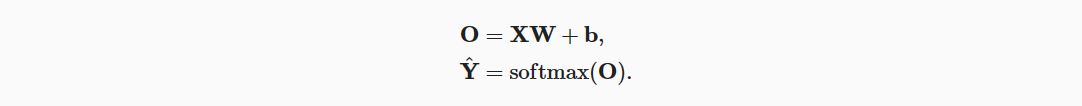
        在 上面的公式中，WX+b的求和会使用广播机制， 小批量的未规范化预测O和输出概率Y^ 都是形状为n×p的矩阵。

        6.损失函数：（利用梯度下降法更新w进而减小损失，当损失越小，纵坐标就越小，当纵坐标接近1的时候，这时候的概率也就是置信度也是最高的。）

        yj是独热编码，0或者1，y^是softmax的值

        

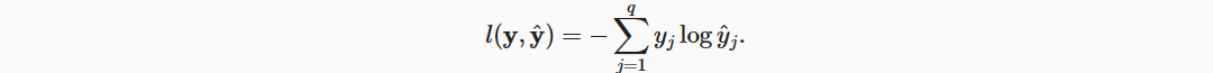
        根据对数函数的性质，加负号是因为在（0，1）区间，其y的值是负数。当y（0 1: # 维度大于1并且列数大于1，跟argmanx匹配 y_hat = y_hat.argmax(axis=1) cmp = y_hat.type(y.dtype) == y return float(cmp.type(y.dtype).sum()) # 0和1，返回总数 # 返回cmp中所有相同索引的和

        10、测试计算准确率这个测试的数据是上面自己人文定义的，准确率是0.5

        print('准确率为{}'.format(accuracy(y_hat, y)/len(y)))
        #准确率为0.5 

        11、计算精度

        传入net是计算y_hat， numel函数是tensor里面数量的的总个数,每次传进去的累加获得预测正确的个数和总个数和总样本数都会保存哎data里面，#metric[0]就是data[0]，每一轮（256一轮）正确的个数除以总，metric[1]是每一轮加256

        def evaluate_accuracy(net, data_iter):
            if isinstance(net, torch.nn.Module):  # 评估模式 只输入后得出结果用来评估模型真确率 不做反向传播
                net.eval()
                # eval()停用dropout和batchnorm
            metric = Accumulator(2)
            # 创建两个元素的列表
            for X, y in data_iter:  #
                metric.add(accuracy(net(X), y), y.numel()) 
           
            return metric[0] / metric[1] 

        12、一轮训练的函数

        def train_epoch_ch3(net, train_iter, loss, updater):
            """训练模型一个迭代周期（定义见第3章）"""
            if isinstance(net, torch.nn.Module):  # 判断是否自己实现函数
                net.train()
            metric = Accumulator(3)
            for X, y in train_iter:
                y_hat = net(X)  # 计算预测值的概率，而且每一行相加等于1
                l = loss(y_hat, y)  # 上面的交叉熵loss
                if isinstance(updater, torch.optim.Optimizer):  # 判断是否自己实现函数
                    updater.zero_grad()
                    l.sum().backward()
                    updater.step()
                else:  # 否则是自己实现的
                    l.sum().backward()
                    updater(X.shape[0])
                metric.add(float(l.sum()), accuracy(y_hat, y), y.numel())
            return metric[0] / metric[2], metric[1] / metric[2]  # 计算这一轮的loss和准确率，还有精度。

        13、训练函数： test_acc = evaluate_accuracy(net, test_iter)是因为每次train完更新w就可以用testdata去看一下效果的变化

        # test_iter用做计算精度
        def train_ch3(net, train_iter, test_iter, loss, num_epochs, updater):
            """训练模型（定义见第3章）"""
            animator = Animator(xlabel='epoch', xlim=[1, num_epochs], ylim=[0.3, 0.9],
                                legend=['train loss', 'train acc', 'test acc'])  # 可视化的Animator
            for epoch in range(num_epochs):  # 测试每一轮的损失，也就是用每一轮的训练好的w和b去与（x，y），把x代入w和b与他的y做预测
                train_metrics = train_epoch_ch3(net, train_iter, loss, updater)
                
                test_acc = evaluate_accuracy(net, test_iter)
                animator.add(epoch + 1, train_metrics + (test_acc,))
            train_loss, train_acc = train_metrics
            # 损失超过0.5报错是因为函数定义中有assert语句，注释掉即可
            assert train_loss  
         
        14、优化函数
         
         
        def updater(batch_size):
            return d2l.sgd([W, b], lr, batch_size)
         
         
        15、预测函数，流程就是 ：用更新后的w和b去预测，然后输入一张图片去预测的话。对所有的类别就行计算，选出概率最大的类别与你输入的图片的标签进行比对，labels（下标）一样的话就正确
         
         
        def predict_ch3(net, test_iter, n=6):
            """预测标签（定义见第3章）"""
            for X, y in test_iter:
                break
            trues = d2l.get_fashion_mnist_labels(y)
           
            preds = d2l.get_fashion_mnist_labels(net(X).argmax(axis=1))
            titles = [true + '\n' + pred for true, pred in zip(trues, preds)]
            d2l.show_images(X[0:n].reshape((n, 28, 28)), 1, n, titles=titles[0:n])
        if __name__ == '__main__':
            lr = 0.1
            num_epochs = 10
            print(train_ch3(net, train_iter, test_iter, cross_entropy, num_epochs, updater))  # 调用前面的函数
            predict_ch3(net, test_iter)
            d2l.plt.show()
         
         
        16、下面运行的结果
         
          
           
            
            
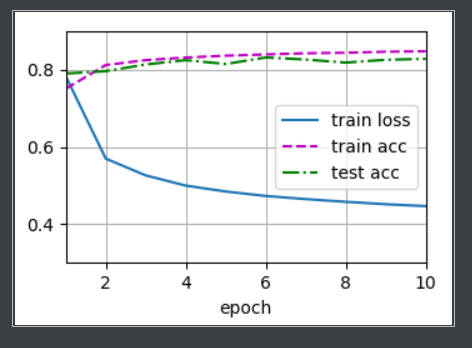
        四：总结
         
         
        这一章节介绍了softmax的理论介绍和实现softmax代码的讲解，下一篇我将会介绍多层感知机，它就是在softmax基础上加了一层隐藏层，并且介绍一些解决欠拟合过拟合的方法和以及解决梯度爆炸和消失的原因以及解决方法
         
         
        所有项目代码+UI界面
         
         
        视频，笔记和代码,以及注释都已经上传网盘，放在主页置顶文章