数据结构：大顶堆、小顶堆

前言：

       堆是其中一种非常重要且实用的数据结构。堆可以用于实现优先队列，进行堆排序，以及解决各种与查找和排序相关的问题。本文将深入探讨两种常见的堆结构：大顶堆和小顶堆，并通过 C++ 语言展示如何实现和使用它们。

1. 什么是大顶堆和小顶堆？

前提：

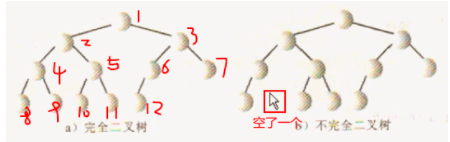
        堆是一种完全二叉树。完全二叉树的定义：所有节点从上往下，从左往右的依次排列，不能有空位置，是为完全二叉树。

        下面是完全二叉树和不完全二叉树的示意图：

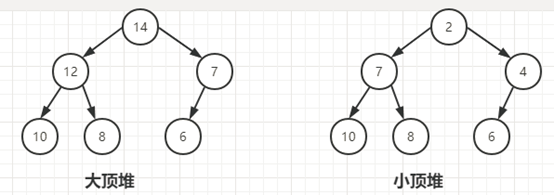
大顶堆：

        根节点（堆顶元素）是所有节点中的最大值（父节点都大于左右子节点）。大顶堆常用于实现优先队列，且可用于构建堆排序算法。

小顶堆：

        小顶堆中的根节点是所有节点中的最小值（父节点都小于左右子节点）。小顶堆常用于问题如：查找流中的前 K 个最小元素。

示意图：

2. 大小顶堆的底层实现

        一般来说，定义二叉树都是定义一个节点类，节点类中包含本节点的数据元素和两个节点指针，分别指向左右子节点，通过这两个节点指针将整个树节点连起来。

代码：

template 
class BstNode
{
public:
	BstNode():leftChild(nullptr), rightChild(nullptr){};
	BstNode(Type _content) :leftChild(nullptr), rightChild(nullptr)
	{
		content = _content;
	};
private:
	Type content;
	BstNode *leftChild;
	BstNode *rightChild;
};

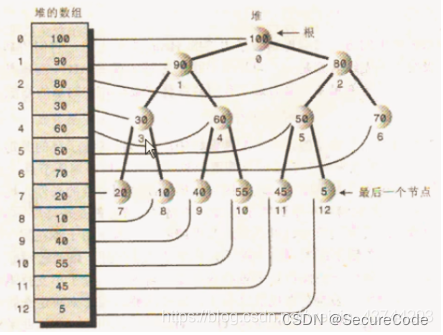
         实际上，堆一般用数组表示，如下图。究其原因，我认为的是通过节点类的方式占用的内存空间多，多加了两个指针。并且当我们做插入操作向上渗透时，需要找到节点的父节点(文章后面会详细描述)，这样实际的节点应该再加一个标识父节点的指针。这样实际是多了3个指针。

图示： 

3. 代码实现小顶堆

3.1 定义小顶堆类

template
class MinHeap
{
public:
	MinHeap(int _maxsize = 10);
	~MinHeap();
	void Push(T _data);//插入数据
	void Pop();//删除堆顶数据
	T& Top();//获取堆顶数据
	void ShowHeap();//打印堆
private:
	T *heap;
	int MaxSize;//堆数组的最大大小
	int currentSize;//堆数组当前大小
};

3.2 构造函数

template
MinHeap::MinHeap(int _maxsize)
:MaxSize(_maxsize)
{
	try{
		if (MaxSize 10->9->8->12依次插入，插入示意图如下： 
 
代码入下：
 
template
void MinHeap::Push(T _data)
{
	if (currentSize == MaxSize){
		//堆满了，扩容
	}
	//将数据放入最后一个位置
	//注意：currentSize和数组索引值差1：
	//比如currentSize = 3，对应的数组索引为2
	//所以，当currentSize=3时，即堆数组有3个数据时，新插入的数据应在数组索引3上
	heap[currentSize] = _data;
	int sonIndex = currentSize;//最后一个位置的数组索引
	int fatherIndex = (currentSize - 1)/ 2;//最后一个位置的父节点的数组索引
	while (sonIndex > 0){
		if (heap[sonIndex]  
        currentSize表示的是当前堆数组有多少个元素。如下图，比如currentSize = 3，表明当前有3个数据。再push一个数据时，在数组的存储的位置刚好是索引3。
 
示意图：
 
        如下图，节点7和节点4的父节点都是节点2。节点7的索引为1，节点4索引为2，节点2的索引为0，所以计算7 4 节点的父节点公式为==（索引-1）/2==，其他节点也一样。这里你不从数组索引角度，从树的层序角度也是一样，只不过公式要变为：层序号/2。
 
扩大堆数组容量
        在上述代码中，当currentSize == MaxSize时，表示堆数组已经满了，此时我们需要扩大数组的大小，这和循环队列和顺序栈是一样的原理。
循环队列：带你一步步用C++实现循环队列
顺序栈：用C++实现顺序栈(以数组为底层数据结构，可自动扩容。
代码如下：
 
template
void MinHeap::ChangeSize()
{
	int size = MaxSize * 2;//堆数组容量扩大1倍
	T* tmp = new T[size];//1.申请一块原来2倍大小的空间。
	std::copy(heap, heap + MaxSize, tmp);//2.将栈中的数据赋值到新的内存空间
	delete[] heap;//3.删除老的空间
	heap = tmp;//4.heap指向新地址
	MaxSize = size;//5.改变MaxSize
}
 
        注意：由于C++编译器是不检查数组越界的，所以，即使程序员不自己扩容，使用越界的索引程序也不会报错，只是它会继续向下占用一块内存。程序员必须注意数组越界的问题。
 
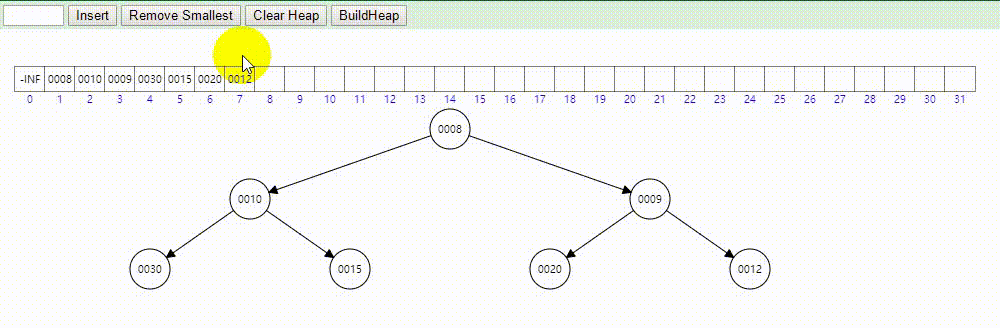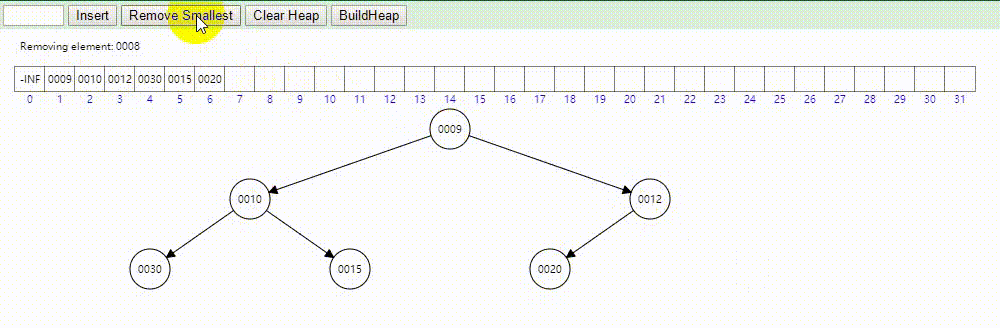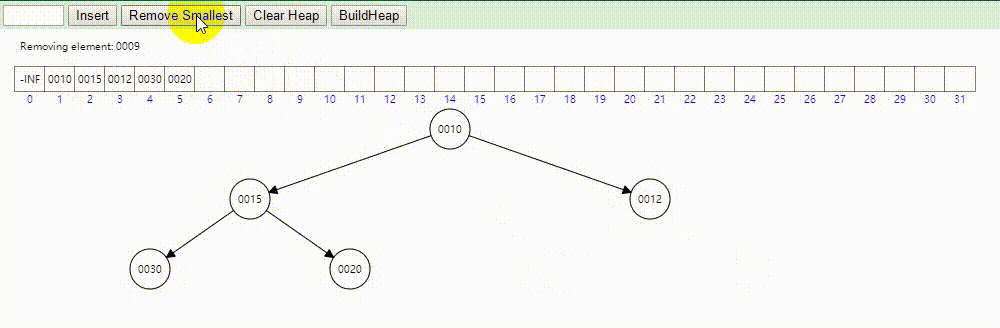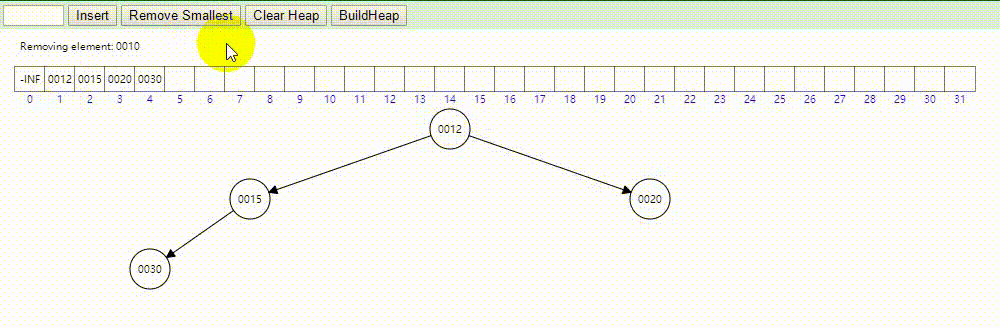
3.4 删除
 
删除步骤：
 
首先把堆顶元素删除
接着把堆的最后一个数据放在堆顶
最后把堆顶数据向下渗透，不断的和两个子节点比较，若父节点不比两个子节点的任意一个小，取两个子节点中小的和父节点交换，一直这样下去，直到父节点比左右子节点都小。
示意图：
 
 
代码如下：
 
template
void MinHeap::Pop()
{
	if (currentSize == 0){
		std::cout  heap[minIndex])
			std::swap(heap[fatherIndex], heap[minIndex]);
		else break;
		fatherIndex = minIndex;
		leftSonIndex = fatherIndex * 2 + 1;
		RightSonIndex = leftSonIndex + 1;
	}
}
 
对于while循环条件说明：
        使用左子节点leftSonIndex和currentSize比较，不要使用右子节点RightSonIndex，因为右子节点RightSonIndex可能没有。当然，你也可以使用父节点fatherIndex和currentSize比较：fatherIndex