假期算法提升(一篇文章带你彻底学会双指针)
温馨提示:这篇文章已超过389天没有更新,请注意相关的内容是否还可用!
呀哈喽,我是结衣。
对于要参加程序设计比赛的人来说,算法永远都是一道绕不开的坎,你必须的去了解他才可以更好的去解决问题。非形式地说,算法就是任何良地计算过程,我们可以把算法看作是用于求良说明地计算问题地工具。那么今天我们学到的就是其中最基础的一种,双指针的应用。
在今天的这篇文章,我们将会了解到双指针的绝大多数题型,掌握了他们,那么你的双指针就算是过关了。文章的题目都是由易到难。在看完解题方法后请先自己敲出代码后再考代码部分哦。
文章目录
- 0.双指针的介绍
- 1.移动零(easy)
- 思路
- 解决方法
- 代码
- 2.复写零(easy)
- 思路
- 解题方法
- 代码
- 3.快乐数(easy)
- 思路
- 解题方法
- 复杂度
- 代码
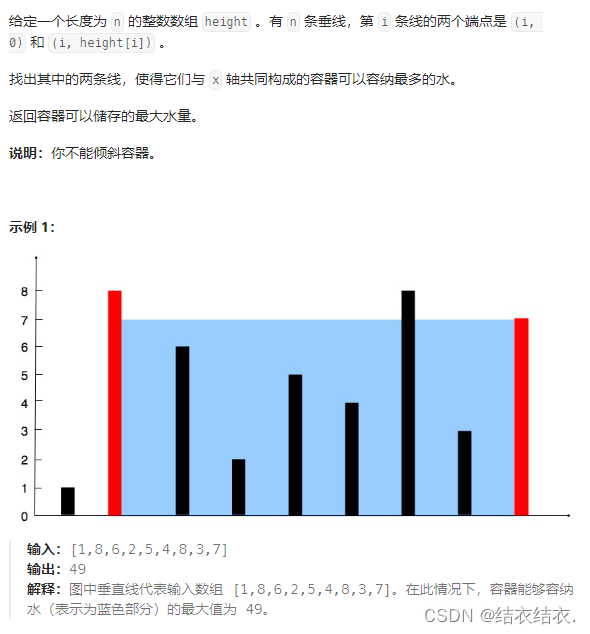
- 4.盛水最多的容器(medium)
- 思路
- 解题方法
- 复杂度
- 代码
- 5.有效的三角形个数(medium)
- 思路
- 解题方法
- 复杂度
- 代码
- 6.查找总价格为目标值的两个商品(easy)
- 思路
- 解题方法
- 复杂度
- 代码
- 7.三数之和(medium)
- 思路
- 解题方法
- 复杂度
- 代码
- 8.四数之和(medium)
- 思路
- 解题方法
- 复杂度
- 代码
- 总结
0.双指针的介绍
常⻅的双指针有两种形式,⼀种是对撞指针,⼀种是左右指针。
对撞指针:⼀般⽤于顺序结构中,也称左右指针。
对撞指针从两端向中间移动。⼀个指针从最左端开始,另⼀个从最右端开始,然后逐渐往中间逼
近。
对撞指针的终⽌条件⼀般是两个指针相遇或者错开(也可能在循环内部找到结果直接跳出循
环),也就是:
left == right(两个指针指向同⼀个位置)
left > right (两个指针错开)
快慢指针:⼜称为⻳兔赛跑算法,其基本思想就是使⽤两个移动速度不同的指针在数组或链表等序列
结构上移动。
这种⽅法对于处理环形链表或数组⾮常有⽤。
其实不单单是环形链表或者是数组,如果我们要研究的问题出现循环往复的情况时,均可考虑使⽤快
慢指针的思想。
快慢指针的实现⽅式有很多种,最常⽤的⼀种就是:
在⼀次循环中,每次让慢的指针向后移动⼀位,⽽快的指针往后移动两位,实现⼀快⼀慢。
1.移动零(easy)
题目链接:移动零
题目描述:
思路
当我们遇到这种需要将数组分为两个模块的时候,我们就可以考虑使用双指针来解决问题。
解决方法
我们用cur指针去扫描整个数组,另一个指针dest去指向cur前最后一个0的位置,每当cur指向非零元素时就交换dest和cur指向的数。
利用这个方法我们就可以把[0,dest]的元素全都转化为非0元素,[dest+1,cur-1]的元素全为0.
了解完方法后先尝试着把代码写出来吧。
代码
class Solution { public: void moveZeroes(vector& nums) { int dest = -1,cur = 0; while(cur if(nums[cur]!=0) { swap(nums[dest+1],nums[cur]); ++dest;++cur; } else ++cur; } } }; public: void duplicateZeros(vector int n = arr.size(); int dest = -1,cur = 0; while(cur if(arr[cur] == 0)dest+=2; else dest+=1; if(dest=n-1)break; cur++; } if(dest == n) { dest--; arr[dest--] = 0; cur--; } while(cur=0) { if(arr[cur] != 0) { arr[dest--] = arr[cur]; } else { arr[dest--] = 0; arr[dest--] = 0; } cur--; } } };3.快乐数(easy)
题目链接:快乐数
题目描述:
思路
运用鸽巢原理(抽屉原理)了解到了解到平方和最后一定会形成一个环,考虑快慢指针。
解题方法
鸽巢原理(抽屉原理):桌上有十个苹果,要把这十个苹果放到九个抽屉里,无论怎样放,我们会发现至少会有一个抽屉里面放不少于两个苹果。这一现象就是我们所说的“抽屉原理”。比如当我们取一个较大数,9999999999,他的各位的平方和位810.远小于他本身,同时这也是100亿内最大的各位平方和。由这个原理,我们就会知道只要循环了811个数,就一定会由重复的数出现然后形成一个环
当然我们也可以把1当成循环
如此一来,快慢指针就发挥作用了,我们让fast指针一次走两个位置,slow指针一次走一个位置,那么可以预见的是,fast一定会先进入到环当中,当slow进入环时,fast也在环中,又因为fast速度更快,那么fast就一定会和slow相遇,我们只需要判断他们相遇的点是否为1就可以了。
复杂度
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1)
代码
class Solution { public: int f(int x) { int sum = 0; while(x) { sum+=pow(x%10,2); x = x/10; } return sum; } bool isHappy(int n) { int fast = n,slow = n; while(1) { fast = f(f(fast)); slow = f(slow); if(fast == slow&&fast == 1) return true; if(fast == slow&&fast!=1) return false; } return false;//因为判断已经在循环中完成了,这里随便返回一个就可以了。 } };4.盛水最多的容器(medium)
题目链接:盛水最多的容器
题目描述:
思路
因为水的面积取决于长乘宽,而长又取决于短的一边。由此我们可以得出假设先以数组的两边为长,再移动左右的长是具有一定的单调性的。
解题方法
我们以示例1为例:
我们先以两端为长,面积为1*8=8
然后我们要移动哪一个呢?如果我们移动较大的一段7
就会发现,面积绝对是变小的,因为,宽在减小,而长一定不会大于1
所以我们会移动较小的一端,直到他们相遇
左右指针,就是这题的解法。
复杂度
时间复杂度: O ( n ) O(n) O(n)
空间复杂度: O ( 1 ) O(1) O(1)
代码
class Solution { public: int maxArea(vector& height) { int left = 0,right = height.size()-1; int sum = 0; while(left if(height[left] sum = max(sum,height[left]*(right-left)); left++; } else { sum = max(sum,height[right]*(right-left)); right--; } } return sum; } }; public: int triangleNumber(vector int n = nums.size(); if(n a = 0;b = c-1; while(a if(nums[a]+nums[b]nums[c]) { res+=b-a; b--; } else a++; } c--; } return res; } }; public: vector int n = price.size(); int left = 0,right = n-1; while(left if(price[left]+price[right]target) right--; else if(price[left]+price[right]price[left],price[right]}; } return {-1,-1};//但是要注意的是因为我们一定会在循环内找到tar,但是外面也是一个返回值要不然不会让你编译成功,所以我们随便返回一个就是了 } }; public: vector vector int left = cur+1,right = n-1; vector if(nums[left]+nums[right] -nums[cur]) right--; else if(nums[left]+nums[right]