动态规划专题——背包问题

🧑‍💻 文章作者：Iareges

🔗 博客主页：https://blog.csdn.net/raelum

⚠️ 转载请注明出处

目录

• 前言
• 一、01背包
• • 1.1 使用滚动数组优化
  • 二、完全背包
  • • 2.1 使用滚动数组优化
    • 三、多重背包
    • • 3.1 使用二进制优化
      • 四、分组背包
      • 总结

        前言

        本文主要介绍常见的四种背包问题，思维导图如下：

        

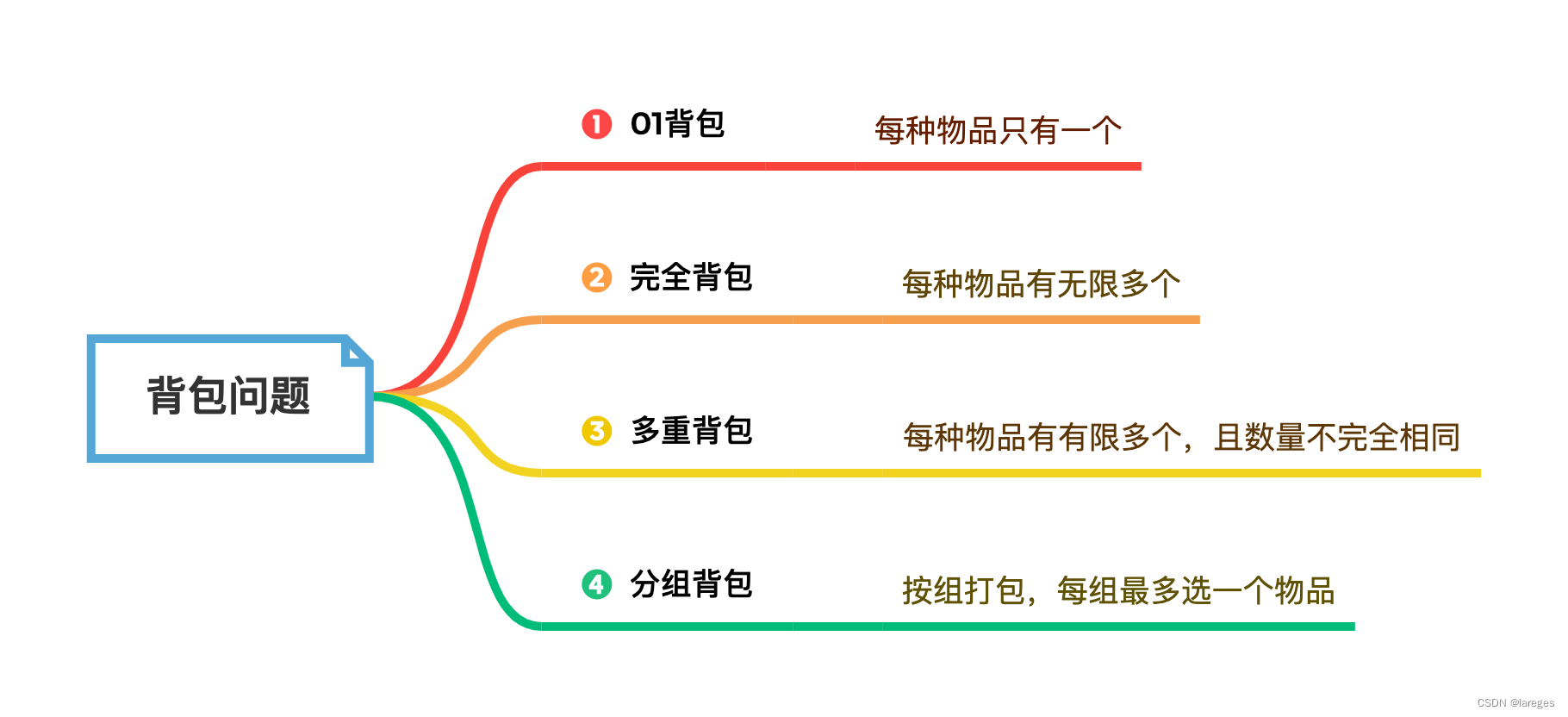
        一、01背包

        💡 现有 N N N 件物品和一个最多能承重 M M M 的背包，第 i i i 件物品的重量是 w i w_i wi​，价值是 v i v_i vi​。在背包能承受的范围内，试问将哪些物品装入背包后可使总价值最大，求这个最大价值。

        因为每件物品只有选与不选两种状态，所以该问题又称01背包问题。

        设 d p [ i ] [ j ] dp[i][j] dp[i][j] 的含义是：在背包承重为 j j j 的前提下，从前 i i i 个物品中选能够得到的最大价值。不难发现 d p [ N ] [ M ] dp[N][M] dp[N][M] 就是本题的答案。

        如何计算 d p [ i ] [ j ] dp[i][j] dp[i][j] 呢？我们可以将它划分为以下两部分：

        • 选第 i i i 个物品：由于第 i i i 个物品一定会被选择，那么相当于从前 i − 1 i-1 i−1 个物品中选且总重量不超过 j − w [ i ] j-w[i] j−w[i]，对应 d p [ i − 1 ] [ j − w [ i ] ] + v [ i ] dp[i-1][j-w[i]]+v[i] dp[i−1][j−w[i]]+v[i]。
        • 不选第 i i i 个物品：意味着从前 i − 1 i-1 i−1 个物品中选且总重量不超过 j j j，对应 d p [ i − 1 ] [ j ] dp[i-1][j] dp[i−1][j]。

          结合以上两点可得递推公式：

          d p [ i ] [ j ] = max ⁡ ( d p [ i − 1 ] [ j ] ,    d p [ i − 1 ] [ j − w [ i ] ] + v [ i ] ) dp[i][j] = \max(dp[i-1][j],\;dp[i-1][j-w[i]]+v[i]) dp[i][j]=max(dp[i−1][j],dp[i−1][j−w[i]]+v[i])

          由于下标不能是负数，所以上述递推公式要求 j ≥ w [ i ] j\geq w[i] j≥w[i]。当 j w[i] >> v[i]; for (int i = 1; i for (int j = 1; j if (j m; for (int i = 1; i int w, v; cin > w >> v; for (int j = m; j >= w; j--) dp[j] = max(dp[j], dp[j - w] + v); } cout ios::sync_with_stdio(false); cin.tie(nullptr); int n, m; cin n >> m; for (int i = 1; i > w[i] >> v[i]; for (int i = 1; i int t = j / w[i]; for (int k = 0; k ios::sync_with_stdio(false); cin.tie(nullptr); int n, m; cin n m; for (int i = 1; i int w, v; cin w >> v; for (int j = w; j ios::sync_with_stdio(false); cin.tie(nullptr); int n, m; cin n > m; for (int i = 1; i int w, v, s; cin > w >> v >> s; for (int j = 1; j int t = min(s, j / w); // 只有这里需要修改 for (int k = 0; k 2i−1,s−2k−1+1(∈[1,2k−1]),​1≤i≤k−1i=k​ ios::sync_with_stdio(false); cin.tie(nullptr); int n, m; cin n m; int cnt = 0; while (n--) { int a, b, s; // a是重量, b是价值, c是数量 cin >> a >> b >> s; for (int k = 1; k cnt++; w[cnt] = a * k, v[cnt] = b * k; s -= k; } if (s 0) { cnt++; w[cnt] = a * s, v[cnt] = b * s; } } n = cnt; for (int i = 1; i = w[i]; j--) dp[j] = max(dp[j], dp[j - w[i]] + v[i]); cout ios::sync_with_stdio(false); cin.tie(nullptr); int n, m; cin n >> m; for (int i = 1; i cin > s[i]; for (int j = 1; j > w[i][j] >> v[i][j]; } for (int i = 1; i = 1; j--) for (int k = 1; k = w[i][k]) dp[j] = max(dp[j], dp[j - w[i][k]] + v[i][k]); cout