C语言：函数递归

                                                    创作不易，给个三连吧！！

一、什么是递归

递归式一种解决问题的方法，在C语言中，递归就是自己调用自己。

递归的思想： 把⼀个⼤型复杂问题层层转化为⼀个与原问题相似，但规模较小的⼦问题来求解；直到⼦问题不能再被拆分，递归就结束了。所以递归的思考⽅式就是把⼤事化小的过程。

递归中的递就是递推的意思，归就是回归的意思

int main()
{
 printf("hehe\n");
 main();//main函数中⼜调⽤了main函数
 return 0;
}

以上就是一个简答的递归程序（自己调用自己），但是最后代码会陷入死递归，导致栈溢出（stack overflow）

所以递归必须要有自己的限制条件！而不能无限制地递归

二、递归的限制条件

为了防止死递归，有2个必要条件：

1、递归存在限制条件，当满足这个条件的时候，递归便不再继续（也就是说，我们要设置让递归停止下来的条件）

2、每次递归的调用要越来越接近这个限制条件（要慢慢让递归停下来）

三、递归的举例

3.1 求n的阶乘

我们知道n的阶乘的公式： n！ =  n ∗ (n − 1)!

这样的思路就是把⼀个较⼤的问题，转换为⼀个与原问题相似，但规模较⼩的问题来求解的。

n!---> n*(n-1)! (n-1)! ---> (n-1)*(n-2)!.... 直到n是1或者0时，不再拆解

再稍微分析⼀下，当 nC                   共3次

3个圆盘    A->C

                 A->B

                 C->B

                 A->C

                 B->A

                 B->C

                 A->C                       共7次

我们发现，最中间的次数恰好就是A->C即最大的圆盘移到C上，中间次数之前相当于将最大圆盘之上的n-1个圆盘放到辅助柱子B上，而中间次数之和的次数相当于将辅助B之上的n-1个圆盘放回C上，所以我们可以得到公式挪动次数：F（n）=F（n-1）+1+F（n-1）即F（n）=F（n-1）*2+1

F(int n)
{
	assert(n>=0);
	if (n==0)
		return 0;
	else
		return 2*F(n - 1)+1;
}

而挪动的过程我们封装2个函数

void Move(char a, char b, int n)
{
	//n代表第几个圆盘，a和b穿得是柱子的编号，表示从a柱子挪到b柱子
	printf("第%d个圆盘从%c柱挪动到%c柱\n", n, a, b);
}
void Hanoi(char a, char b, char c, int n)
//a表示圆盘所在的柱子，b表示移动圆盘的辅助柱子，c表示圆盘的目标柱子，n表示圆盘的个数
{
	assert(n >= 0);
	if (n ==1)
		Move(a, c, n);//直接将圆盘放到c上
	else
	{
		Hanoi(a, c, b, n - 1);//将前面n-1个圆盘通过C先挪动到B上
		Move(a, c, n);//将第n个圆盘放到c上
		Hanoi(b, a, c, n - 1);//将b上的n-1个圆盘通过a挪动到c上
	}
}

最后通过这三个函数完成计算汉诺塔问题的挪动次数以及挪动的过程！！

F(int n)//计算挪动次数
{
	assert(n>=0);
	if (n==0)
		return 0;
	else
		return 2*F(n - 1)+1;
}
void Move(char a, char b, int n)
{
	//n代表第几个圆盘，a和b穿得是柱子的编号，表示从a柱子挪到b柱子
	printf("第%d个圆盘从%c柱挪动到%c柱\n", n, a, b);
}
void Hanoi(char a, char b, char c, int n)
//a表示圆盘所在的柱子，b表示移动圆盘的辅助柱子，c表示圆盘的目标柱子，n表示圆盘的个数
{
	assert(n > 0);
	if (n == 1)
		Move(a, c, n);//将圆盘直接移动到c上
	else
	{
		Hanoi(a, c, b, n - 1);//将前面n-1个圆盘通过C先挪动到B上
		Move(a, c, n);//将第n个圆盘放到c上
		Hanoi(b, a, c, n - 1);//将b上的n-1个圆盘通过a挪动到c上
	}
}
int main()
{
	int n = 0;
	scanf("%d", &n);//输入圆盘数量
	char src = 'A';//a代表圆盘所在的柱子
	char ass = 'B';//b代表a->c的辅助柱子
	char dst = 'C';//c代表圆盘的目标柱子
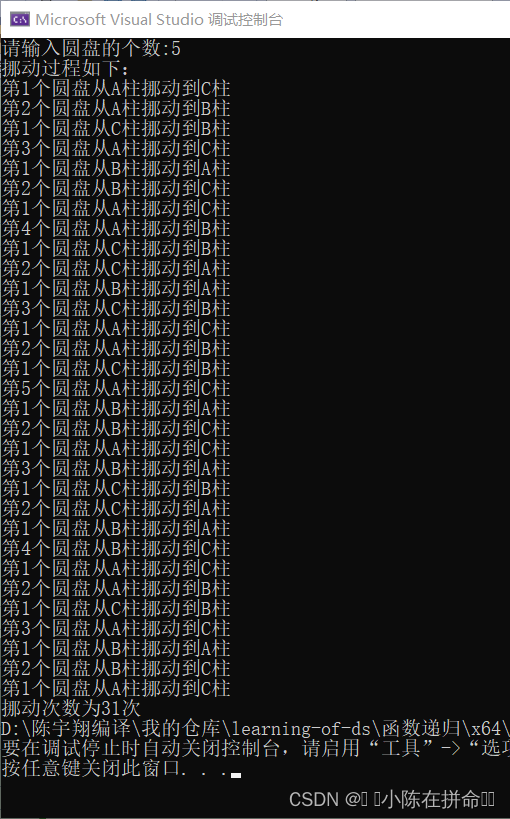
	printf("挪动过程如下：\n");
	Hanoi(src,ass,dst, n);//挪动过程
	printf("挪动次数为%d次", F(n));//挪动次数
	return 0;
}

6.3 求1-n的全排列

      比如1、2、3、4、5，为了实现全排列，我们先将他放在一个数组中，我们先取第1个数，如果第1个数确定为2，那么第1个数是2的全排列就即为1345的全排列，第2个数可以取1345中的1个数，又可以等价于后三个数的全排列，以此类推……

因此，n个数的全排列=确定的第一位+（n-1）个数全排列=确定的前两位+（n-2）个数全排列=............

其中，确定某位是某数这一操作由——与后面的数依次交换-递归-换回——实现。

int count = 0;//利用全局变量计算总次数
void swap(int arr[], int a, int b)//交换下标为a  b的两个数
{
	int temp = arr[a];
	arr[a] = arr[b];
	arr[b] = temp;
}
void Perm(int arr[], int begin, int n)//n为最后一个数的角标，begin为数组从下标为几的数字开始
{
	assert(n > 0);
	if (begin == n)
	{	//如果begin为最后一个元素开始，说明该层递归已经结束了,此次数组的顺序就是全排列的顺序
		for (int i = 0; i