用遗传算法解决多目标优化和非线性规划问题（MATLAB）

一、多目标优化

        简单来说多目标优化就是目标函数不止一个，需要注意一下两点：

        （1）决策变量需要与每个目标函数存在关联；

        （2）目标函数之间需要存在冲突，比如有两个目标函数，当一个目标函数变大时另一个目标函数一定会变小。

解决方法1：将多目标转换为单目标

        目标函数=权重1*目标1+权重2*目标2+……        （权重可以人为设置，也可以通过一些评价性方法获得，比如双权法、判断矩阵打分）

解决方法2：pareto前沿

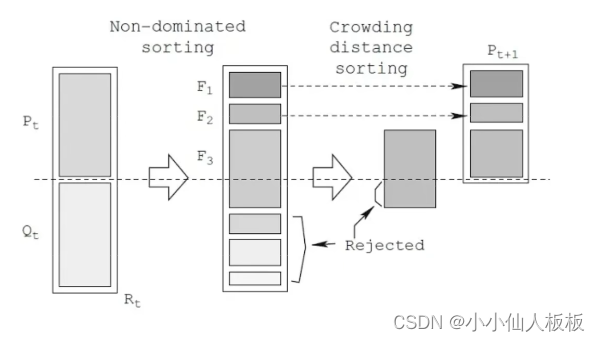
NSGA-II,非支配排序遗传算法

• 支配（dominance）：在多目标优化问题中，如果个体p至少有一个目标比个体q好，而且个体p的所有目标都不比q差，那么称个体p支配个体q
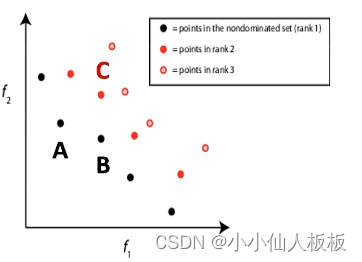
• 序值（rank):如果p支配q，那么p的序值比q低；如果p、q互不支配，那么p、q有相同的序值。
• 拥挤距离：表示个体之间的拥挤程度，测量相同序值个体之间的距离（选择时可以尽量少的选择拥挤距离小的点）

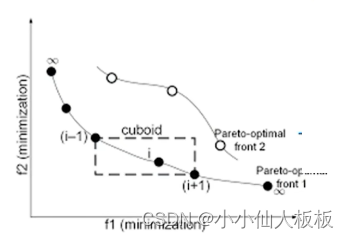
   算法流程图

  

  gamultiabj函数

  （1）gamultiabj函数与传统GA的区别：

          传统GA总是偏爱适应值（等级）更好的个体，受控的精英GA也偏爱安歇可以帮助种群增加多样性的个体，即使他们的适应值较低。也就是说传统的GA只选取序值靠前的个体，而受控的精英GA还会选择一部分序值靠后的个体。

  （2）迭代

  • 选择父代：唯一可用的方法二元锦标赛，也可以自定义选择功能。
  • 交叉、变异、从选定的父代创建子代
  • 将当前种群喊个子代组合成一个新矩阵（种群），即拓展种群
  • 计算拓展种群中所有个体的等级（rank）和拥挤距离
  • 通过保留每个等级（rank）的适当数量的个体来修剪拓展后的种群（与传统的NSGA的重要区别）

                     ParetoFraction（帕累托集比例）：当求解器从更高的前沿选择个体时，设置保持在第一个Pareto前沿的个体比例。此选项是0-1之间的标量。第一个帕累托前沿的个人分数可以超过此比例（其他等级的个体数量太少时会出现这个情况）。

    二、非线性规划

            目标函数或者约束条件中有一个或者几个非线性函数

    三、实例

    带限制条件的双目标优化

    题目：min         F(x)=[objective1(x);objective2(x)]

               x

               -1.5