深度学习指标| 置信区间、Dice、IOU、MIOU、Kappa

深度学习部分指标介绍

• 置信区间
• 混淆矩阵
• Dice
• IOU和MIOU
• Kappa

  置信区间

  95%CI指标

  读论文的时候，常会看到一个“95%CI”的评价指标。

  其中CI指的是统计学中的置信区间（Confidence interval，CI）。在统计学中，一个概率样本的置信区间，是对产生这个样本的总体的参数分布中的某一个未知参数值，以区间形式给出的估计。

  这样解释有点抽象，直观理解可以为“用样本估计总体平均值，给出总体均值最有可能落的区域”。

  置信区间怎么得到？

  下面用一个例子理解来最直观理解一下“置信区间”得到的过程。

  一个10人的班级，这是每个人考的分数。

  学生1	学生2	学生3	学生4	学生5	学生6	学生7	学生8	学生9	学生10
  60	70	80	90	66	72	88	91	65	75

  在已经知道全部学生成绩的时候，可以很好推出平均值为75.7。

  但是现实生活中，通常需要计算的总体数量很大，我们是没办法在上帝视角下知道总体所有的值，例如需要知道全市所有学生的平均成绩，这个时候我们只能采用抽样的方式来估计。

  从这10个人里，取出3个人作为抽样标本并计算其平均值，取5组。

  • 学生1、2、5：65.3
  • 学生3、4、8：87
  • 学生4、6、7：83.3
  • 学生7、8、9：81.3
  • 学生3、6、9：72.3

    每次抽样取平均值实际上就是在对全部学生平均成绩的一次点估计，点估计估计一个值，笃定了这个值是精确。

    但是这五次点估计，在不知道总体学生成绩的时候，我们也依旧不知道那个是最接近真实平均值的。

    于是就有区间估计，区间估计估计了一个范围，认为这个区间内至少有一个值使得待定参数最接近于真实值。通常可以用点估计算出来的数据加上一个变动幅度形成一个区间。

    但是就算估计出来了区间，也有可能这个区间未必包含或者很靠近真实平均值，依旧还是不知道那个是最好的区间。

    于是又有了置信区间来知道这个区间范围包含真实值的可信度，来评估区间的好坏。

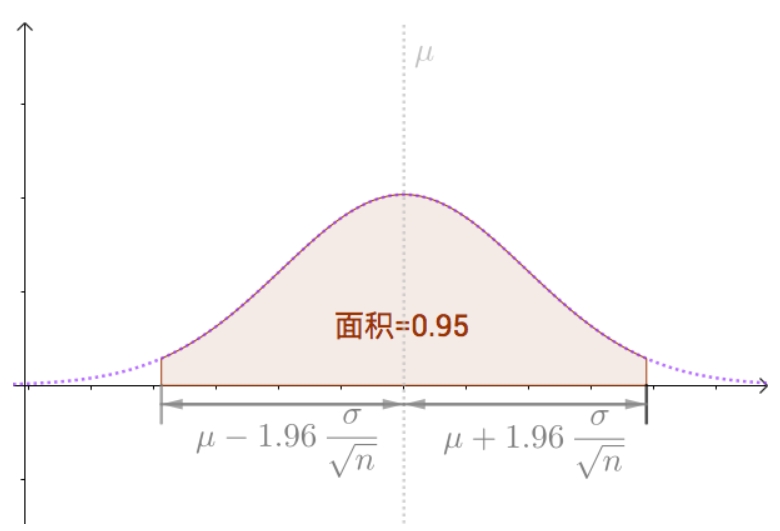
    根据大数定理和中心极限定律，样本均值M服从正态分布：

    M ∼ N ( μ , σ 2 n ) M\sim N(\mu,\frac{{\sigma}^2}{n}) M∼N(μ,nσ2​)

    以 μ \mu μ为中心， σ \sigma σ是总体分布的标准差，面积为0.95的区间就是置信区间。95%置信区间可以理解为对总体抽样1000次，然后发现95%抽样均值分布在这个区间中。

    

    但实际情况中我们是不知道真实的 μ \mu μ是多少的，可以用抽样样本均值替代。

    混淆矩阵

    因为后面说Dice、IOU和MIOU要用到混淆矩阵的一些概念，所以放在这里方便理解。

    	预测为正类别	预测为负类别
    实际为正类别	True Positive (TP)	False Negative (FN)
    实际为负类别	False Positive (FP)	True Negative (TN)

    混淆矩阵中TP、TN、FP、FN：

    TP（True Positives）：预测为正类别，并且预测对了

    TN（True Negatives）：预测为负类别，而且预测对了

    FP（False Positives）：预测为正类别，但是预测错了

    FN（False Negatives）：预测为负类别，但是预测错了

    Dice

    Dice系数又叫做骰子系数，作用在于计算两个集合相似度，取值范围在[0,1]。

    对于集合X和集合Y的Dice系数计算公式可以写成：

    D i c e ( X , Y ) = 2 ∗ ∣ X ∩ Y ∣ ∣ X ∣ + ∣ Y ∣ Dice(X,Y)=\frac{2*|X\cap Y|}{|X|+|Y|} Dice(X,Y)=∣X∣+∣Y∣2∗∣X∩Y∣​

    对于混淆矩阵中，Dice系数的表述可以看作是预测为正类的集合与真实正类集合两者之间的相似度。

    Dice系数计算公式可以写成：

    D i c e = 2 ∗ T P ( T P + F N ) + ( T P + F P ) Dice=\frac{2*TP}{(TP+FN)+(TP+FP)} Dice=(TP+FN)+(TP+FP)2∗TP​

    

    IOU和MIOU

    IOU（Intersection over Union）是交并比，MIOU（Mean Intersection over Union）指平均交并比，也称为平均IOU。两个都是用于衡量语义分割任务中预测结果与真实标签之间的相似度。

    图像语义分割是像素级别上的分类，每个像素都被赋予一个特定的类别标签。可以把每个类别的预测结果和真是标签分别视为两个二值图像，IOU交并比是计算两个之间重叠区域与它们的并集之间的比例，来衡量相似度。

    I O U = ∣ X ∩ Y ∣ ∣ X ∪ Y ∣ IOU=\frac{|X\cap Y|}{|X\cup Y|} IOU=∣X∪Y∣∣X∩Y∣​

    

    IOU=某类别的交集区域 / 某类别的并集区域

    MIOU = 所有类别的IoU之和 / 类别总数

    例如一张图片可以分为两个标签分别是背景和人，则MIOU=(IOU人+IOU背景)/2

    Kappa

    Kappa系数是一个用于一致性检验的指标，可用于衡量分类的效果，取值范围在[-1,1]。

    一致性通常指模型的预测结果和实际分类结果是否一致。

    Kappa系数的计算公式可以写成：

    K a p p a = p 0 − p e 1 − p e Kappa=\frac{p_0-p_e}{1-p_e} Kappa=1−pe​p0​−pe​​

    其中 p 0 p_0 p0​是总体分类精度，每一类正确分类的样本数量之和除以总样本数。

    设每一类的真实样本个数分别为 a 1 、 a 2 . . . a_1、a_2... a1​、a2​...，而预测出来的每一类的样本个数分别为 b 1 、 b 2 . . . b_1、b_2... b1​、b2​...，则 p e = a 1 × b 1 + a 2 × b 2 . . . n × n p_e=\frac{a_1×b_1+a_2×b_2...}{n×n} pe​=n×na1​×b1​+a2​×b2​...​

    虽然说Kappa系数取值范围在[-1,1]，但是通常落在[0,1]，根据结果通常可以分成五个级别的一致性：

    • 极低的一致性（slight）：0.0~0.20
    • 一般的一致性（fair）：0.21~0.40
    • 中等的一致性（moderate）：0.41~0.60
    • 高度的一致性（substantial）：0.61~0.80
    • 几乎完全一致（almost perfect）： 0.81~1