Python算法100例-3.6 自守数

1．问题描述

自守数是指一个数的平方的尾数等于该数自身的自然数。例如， 5 2 = 25 ， 2 5 2 = 625 ， 7 6 2 = 5776 ， 937 6 2 = 87909376 5^2=25，25^2=625，76^2=5776，9376^2=87909376 52=25，252=625，762=5776，93762=87909376。求100000以内的自守数

2．问题分析

根据自守数的定义，求解本题的关键是知道当前所求自然数的位数，以及该数平方的尾数与被乘数、乘数之间的关系。

3．算法设计

采用“求出一个数的平方后再截取最后相应位数”的方法显然是不可取的，因为计算机无法表示过大的整数。

分析手工方式下整数平方（乘法）的计算过程，以376为例：

本问题所关心的是积的最后三位。分析产生积的后三位的过程可以看出，在每一次的部分积中，并不是它的每一位都会对积的后三位产生影响。总结规律可以得到，在三位数乘法中，对积的后三位产生影响的部分积分别如下：

·第一个部分积中：被乘数最后三位×乘数的倒数第一位。

·第二个部分积中：被乘数最后两位×乘数的倒数第二位。

·第三个部分积中：被乘数最后一位×乘数的倒数第三位。

将以上部分积的后三位求和后截取后三位就是三位数乘积的后三位。这样的规律可以推广到同样问题的不同位数乘积。

4．求给定数的位数

求一个数的位数可以借助最高位的权值来计算，对于十进制来说，个位的权值为100，十位的权值为101，百位的权值为102，以此类推。一个存储三位数的变量n=123，每次除以10，将得到的值再赋给n，直到n的值为0，最多可以除3次；若变量n中存储的是4位数，用同样的方法去除以10最多可以除4次。可以发现，直到变量变为0，除以10的次数即为当前给定数的位数。程序如下：

# 求给定数的位数
if __name__=="__main__":
    print("请输入一个正整数n：", end="")
    n = int(input())
    if n  0:                       # 由number的位数确定截取数字进行乘法时的系数k
    mul //= 10
    k *= 10

5．分离给定数中的最后几位

从一个两位数（存在变量n中）开始分析，分离最低位个位：n%10；对于三位数n，分离最后两位：n%100；对于四位数n，分离最后三位：n%1000；以此类推，若分离出最后x位，只需要用原数对10x求余。

从算法设计部分所举例子可以看出，对于第二个部分积“2632”来说其实应该是“26320”，因为对于乘数中的倒数第二位“7”来说，因其在十位，对应的权值为10，第二个部分积实质上为376×70=26 320。故求部分积的程序段为：

while k > 0:
    # (部分积+截取被乘数的后N位×截取乘数的第M位)，%a再截取部分积
    mul = (mul + (number % (k * 10))*(number % b - number % (b //  10)))%a
    k //= 10                                # k为截取被乘数时的系数
    b *= 10

对于整个循环来说，变量k是由number的位数确定截取数字进行乘法时的系数。第一次执行循环体时，被乘数的所有位数都影响到平方的尾数，故第一个部分的积等于被乘数×乘数的最后一位，将部分积累加到变量mul上，再对a取余截取相应的尾数位数；第二次执行循环体，影响平方尾数的是被乘数中除了最高位之外的数（故k先除以10再参加运算），第二个部分的积等于被乘数×乘数的倒数第二位，(number%b-number%(b//10))用来求乘数中影响平方尾数的对应位上的数；第三次、第四次执行循环体的过程同上。

6．确定程序框架

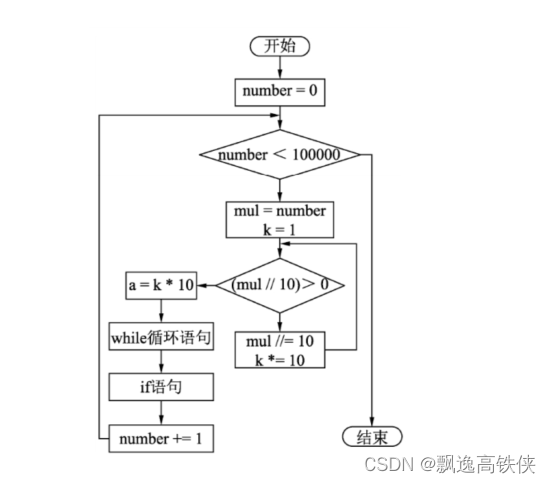
该程序的简略流程图如图所示。

7．完整的程序

%%time
#  自守数
if __name__=="__main__":
    print("100000以内的自守数：")
    for number in range(0, 100000):
        mul = number
        k = 1
        while (mul // 10) > 0:   # 由number的位数确定截取数字进行乘法时的系数k
            mul //= 10
            k *= 10
        a = k * 10  # a为截取部分积时的系数
        mul = 0 # 积的最后n位
        b = 10  # b为截取乘数相应位时的系数
        while k > 0:
            # (部分积+截取被乘数的后N位*截取乘数的第M位)，%a再截取部分积
            mul = (mul + (number % (k * 10))*(number % b - number % (b //  10)))%a
            k //= 10  # k为截取被乘数时的系数
            b *= 10
        if number == mul:  # 判定若为自守数则输出
            print("%ld " %number, end="\t")
    print('\n')

100000以内的自守数：
0 	1 	5 	6 	25 	76 	376 	625 	9376 	90625 	CPU times: user 536 ms, sys: 2.14 ms, total: 539 ms
Wall time: 535 ms